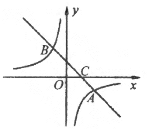
题目内容
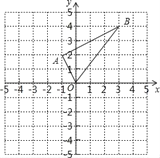
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于
的图像交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)请直接写出不等式![]() 的解集;
的解集;
(3)将![]() 轴下方的图像沿
轴下方的图像沿![]() 轴翻折,点
轴翻折,点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)k![]() =8,n=4;(2)2<x<0或x>4;(3)8.
=8,n=4;(2)2<x<0或x>4;(3)8.
【解析】
(1)将A点坐标代入![]() ;
;
(2)用函数的观点将不等式问题转化为函数图象问题;
(3)求出对称点坐标,求面积.
(1)将A(4,2)代入![]() ,得k
,得k![]() =8.
=8.
∴y=![]() ,
,
将(2,n)代入y=![]() ,
,
n=4.
∴k![]() =8,n=4;
=8,n=4;
(2)根据函数图象可知:2<x<0或x>4;
(3)将A(4,2),B(2,4)代入![]() ,得k
,得k![]() =1,b=2
=1,b=2
∴一次函数的关系式为y=x+2
与x轴交于点C(2,0)
∴图象沿x轴翻折后,得A′(4,2),
S![]() =(4+2)×(4+2)×
=(4+2)×(4+2)×![]()
![]() ×4×4
×4×4![]() ×2×2=8
×2×2=8
∴△A′BC的面积为8.

练习册系列答案
相关题目
【题目】某童装厂现有甲种布料38米,乙种布料26米,现计划用这两种布料生产L.M两种型号的童装共50套.已知做一套L.M型号的童装所需用布料和所获得利润如下表:
甲种布料 | 乙种布料 | 获 利 | |
L型 | 0.5米 | 1米 | 45元 |
M型 | 0.9米 | 0.2米 | 30元 |
假设L型号的服装生产![]() 套,请你写出满足题意的不等式组,求出其解集;并根据计算结果,设计生产方案.
套,请你写出满足题意的不等式组,求出其解集;并根据计算结果,设计生产方案.