题目内容
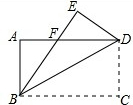 如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,CD=3cm,CB=4cm,则△BFD的面积为
如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,CD=3cm,CB=4cm,则△BFD的面积为考点:翻折变换(折叠问题)
专题:计算题
分析:先根据矩形的性质得AB=CD=3,AD=BC=4,AD∥BC,再根据折叠的性质得∠DBC=∠DBF,由AD∥BC得∠DBC=∠BDF,所以∠BDF=∠FBD,根据等腰三角形的判定得FB=FD,设FD=x,则FB=x,AF=4-x,在Rt△ABF中,根据勾股定理得到32+(4-x)2=x2,解得x=
,然后根据三角形面积公式求解.
| 25 |
| 8 |
解答:解:∵四边形ABCD为矩形,
∴AB=CD=3,AD=BC=4,AD∥BC,
∵矩形纸片ABCD沿对角线BD折叠,点C落在点E处,
∴∠DBC=∠DBF,
∵AD∥BC,
∴∠DBC=∠BDF,
∴∠BDF=∠FBD,
∴FB=FD,
设FD=x,则FB=x,AF=4-x,
在Rt△ABF中,∵AB2+AF2=BF2,
∴32+(4-x)2=x2,
解得x=
,
∴DF=
,
∴△BFD的面积=
AB•DF=
•3•
=
(cm2).
故答案为
cm2.
∴AB=CD=3,AD=BC=4,AD∥BC,
∵矩形纸片ABCD沿对角线BD折叠,点C落在点E处,
∴∠DBC=∠DBF,
∵AD∥BC,
∴∠DBC=∠BDF,
∴∠BDF=∠FBD,
∴FB=FD,
设FD=x,则FB=x,AF=4-x,
在Rt△ABF中,∵AB2+AF2=BF2,
∴32+(4-x)2=x2,
解得x=
| 25 |
| 8 |
∴DF=
| 25 |
| 8 |
∴△BFD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 25 |
| 8 |
| 75 |
| 16 |
故答案为
| 75 |
| 16 |
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
代数式a-2与1-2a的值相等,则a等于( )
| A、0 | B、1 | C、2 | D、3 |
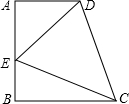 在直角梯形ABCD中,AD∥BC,(AD<BC),AB⊥BC,AB=BC=12,点E在AB边上,连接CE,DE,若∠DCE=45°,DE=10,则线段BE的长为
在直角梯形ABCD中,AD∥BC,(AD<BC),AB⊥BC,AB=BC=12,点E在AB边上,连接CE,DE,若∠DCE=45°,DE=10,则线段BE的长为