Question

如图，将一块斜边长为12cm，∠B=60°的直角三角板ABC，绕点C沿逆时针方向旋转90°至△′B′C′的位置，再沿CB向右平移，使点B′刚好落在斜边AB上，那么此三角板向右平移的距离是（　　）

• A、6-2

  3

• B、2

  3

• C、4-

  3

• D、3

Answer 1

考点：旋转的性质,平移的性质

专题：计算题

分析：过点B′作BC的平行线交AB于B″，如图，在Rt△ABC中利用含30度的直角三角形三边的关系得到BC=

1

2

AB=6，AC=

3

BC=6

3

，再根据旋转的性质得∠A′CA=90°，CB′=CB=6，则可计算出AB′=AC-CB′=6

3

-6，由B′B″∥BC得∠AB′B″=90°，然后在Rt△AB′B″中计算出B′B″=

3

3

AB′=6-2

3

，于是可判断此三角板向右平移的距离为（6-2

3

）cm．

解答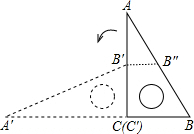：解：过点B′作BC的平行线交AB于B″，如图，
在Rt△ABC中，∵∠B=60°，
∴∠A=30°，
∴BC=

1

2

AB=

1

2

×12=6，
∴AC=

3

BC=6

3

，
∵△ABC，绕点C沿逆时针方向旋转90°至△′B′C′的位置，
∴∠A′CA=90°，CB′=CB=6，
∴点A′、C、B共线，AB′=AC-CB′=6

3

-6，
∵B′B″∥BC，
∴∠AB′B″=90°，
在Rt△AB′B″中，∵∠A=30°，
∴B′B″=

3

3

AB′=

3

3

×（6

3

-6）=6-2

3

，
即此三角板向右平移的距离为（6-2

3

）cm．
故选A．

点评：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了平移的性质．