题目内容
6.设AB、CD是⊙O的两条弦,AB∥CD,若⊙O的半径为10,AB=16,CD=12,则AB与CD之间的距离为2或14.分析 分两种情况进行讨论:①弦AB和CD在圆心同侧;②弦AB和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可,小心别漏解.
解答 解:①当弦AB和CD在圆心同侧时,如图,
∵AB=16,CD=12,
∴AE=8,CF=6,
∵OA=OC=10,
∴EO=6,OF=8,
∴EF=OF-OE=2;
②当弦AB和CD在圆心异侧时,如图,
∵AB=16,CD=12,
∴AF=8,CE=6,
∵OA=OC=10,
∴OF=6,OE=8,
∴EF=OF+OE=14.
∴AB与CD之间的距离为14或2.
故答案为:2或14.
点评 本题考查了勾股定理和垂径定理的应用.此题难度适中,解题的关键是注意掌握数形结合思想与分类讨论思想的应用,小心别漏解.

练习册系列答案
相关题目
17.已知a,b互为相反数,则下列各组数中不是互为相反数的是( )
| A. | -2a和-2b | B. | 2a和2b | C. | a+1和b+1 | D. | a+1和b-1 |
14.下列说法中,正确的是( )
| A. | 全等图形是形状相同的两个图形 | |
| B. | 全等三角形是指面积相同的两个三角形 | |
| C. | 等边三角形都是全等三角形 | |
| D. | 全等图形的周长、面积都相等 |
 如图,已知△ABE≌△ADC,∠1=36°,∠DAE=76°,∠B=25°.求∠DAC、∠C的度数.
如图,已知△ABE≌△ADC,∠1=36°,∠DAE=76°,∠B=25°.求∠DAC、∠C的度数.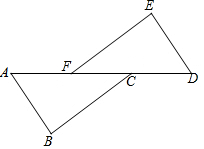 如图所示,已知AF=DC,BC∥EF,AB∥DE,求证:△ABC≌△DEF.
如图所示,已知AF=DC,BC∥EF,AB∥DE,求证:△ABC≌△DEF.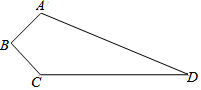 如图四边形ABCD是实验中学的一块空地的平面图,其中∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m现计划在空地上植上草地绿化环境,若每平方米的草皮需150元;问需投入资金多少元?
如图四边形ABCD是实验中学的一块空地的平面图,其中∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m现计划在空地上植上草地绿化环境,若每平方米的草皮需150元;问需投入资金多少元?