题目内容
解方程.
(1)x2-3x=0.
(2)x2+5x-6=0.
(1)x2-3x=0.
(2)x2+5x-6=0.
考点:解一元二次方程-因式分解法
专题:
分析:(1)利用提取公因式法对等式的左边进行因式分解;
(2)利用“十字相乘法”对等式的左边进行因式分解.
(2)利用“十字相乘法”对等式的左边进行因式分解.
解答:解:(1)分解因式得:x(x-3)=0,
可得:x=0或x-3=0,
解得:x1=0,x2=3.
(2)∵x2+5x-6=0,
∴(x-1)(x+6)=0,
即x-1=0或x+6=0,
解得:x1=1,x2=-6.
可得:x=0或x-3=0,
解得:x1=0,x2=3.
(2)∵x2+5x-6=0,
∴(x-1)(x+6)=0,
即x-1=0或x+6=0,
解得:x1=1,x2=-6.
点评:此题考查了解一元二次方程-因式分解法,利用因式分解法解方程时,首先将方程右边化为0,左边化为积的形式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
在
,
,
,
,
,a+
中,分式的个数是( )
| 1 |
| x |
| 1 |
| 2 |
| x(x2+1) |
| x |
| 3xy |
| π |
| 3 |
| x+y |
| 1 |
| m |
| A、2 | B、3 | C、4 | D、5 |
如果-
a2b2n-1是五次单项式,则n的值为( )
| π |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
 设A是函数y=
设A是函数y= 如图,是由6个相同的长方体堆成的物体,试画出这一物体的主视图、左视图、俯视图.
如图,是由6个相同的长方体堆成的物体,试画出这一物体的主视图、左视图、俯视图.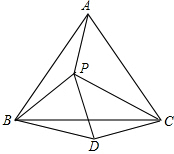 已知:如图,点P是等边△ABC内的一点,连结PA,PB,PC,以BP为边作等边△BPD,连结CD.
已知:如图,点P是等边△ABC内的一点,连结PA,PB,PC,以BP为边作等边△BPD,连结CD.