题目内容
2．若x=-1是关于x的方程x2+mx-1=0的一个根，则m的值是（ ）| A． | 0 | B． | 1 | C． | 2 | D． | -2 |
分析 把x=-1代入方程x2-mx-1=0得到一个关于m的一元一次方程，求出方程的解即可．
解答 解：把x=-1代入方程x2-mx-1=0，
得：1+m-1=0，
解方程得：m=0．
故选A．
点评 本题主要考查对解一元一次方程，等式的性质，一元二次方程的解等知识点的理解和掌握，能得到方程1+m-1=0是解此题的关键．
练习册系列答案
相关题目
12．下列代数式中符合书写要求的是（ ）
| A． | ab4 | B． | 4$\frac{1}{3}$m | C． | x÷y | D． | -$\frac{5}{2}$a |
13．已知四条线段满足$a=\frac{cd}{b}$，将它改写成为比例式，下面正确的是（ ）
| A． | $\frac{a}{b}=\frac{c}{d}$ | B． | $\frac{a}{c}=\frac{b}{d}$ | C． | $\frac{a}{c}=\frac{d}{b}$ | D． | $\frac{a}{d}=\frac{b}{c}$ |
10．
请你用学习“一次函数”时积累的经验和方法解决下列问题：
（1）在平面直角坐标系中，画出函数y=|x|的图象：
①列表填空：
②描点、连线，画出y=|x|的图象；
（2）结合所画函数图象，写出y=|x|两条不同类型的性质；
（3）写出函数y=|x|与y=|x+2|图象的平移关系．
请你用学习“一次函数”时积累的经验和方法解决下列问题：（1）在平面直角坐标系中，画出函数y=|x|的图象：
①列表填空：
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | … |
（2）结合所画函数图象，写出y=|x|两条不同类型的性质；
（3）写出函数y=|x|与y=|x+2|图象的平移关系．
如图，学校打算用长为16cm的篱笆围成一个长方形的生物园饲养小兔，生物园一面靠墙（篱笆只需围三面，AB为宽）；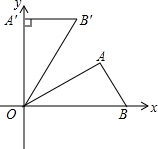
如图，在平面直角坐标系中，Rt△OAB的斜边OB在x轴的正半轴上，点A在第一象限，将△OAB，使点O按逆时针方向旋转至△OA′B′，使点A的对应点A′落在y轴的正半轴上，已知OB=2，∠AOB=30°．