题目内容
5．已知抛物线y=x2+mx+m的顶点在直线y=-x上，求m的值．分析 根据题意可以求得抛物线的顶点坐标，然后将顶点坐标代入y=-x，从而可以求得m的值．
解答 解：∵y=x2+mx+m=（x+$\frac{1}{2}$m）2-$\frac{{m}^{2}}{4}$+m，
∴抛物线y=x2+mx+m的顶点坐标是（-$\frac{1}{2}$m，-$\frac{{m}^{2}}{4}$+m），
∵抛物线y=x2+mx+m的顶点在直线y=-x上，
∴-$\frac{{m}^{2}}{4}$+m=$\frac{1}{2}$m，
解得，m=0或m=2．
点评 本题考查二次函数的性质、一次函数图象上点的坐标特征，解题的关键是明确题意，利用数形结合的思想解答．
练习册系列答案
相关题目
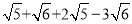时我们可以将式子中的
、
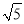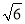分别看成两个相同的字母a、b；则原式可看成a+b+2a﹣3b，我们用类比合并同类项的方法可将上面的式子化简．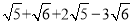
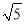+（1-3）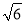
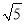﹣2
|
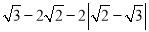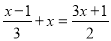时，方程两边同时乘以6，去分母后，正确的是（ ）
如图，由4个小正方形组成的田字格，△ABC的顶点都是小正方形的顶点，在田字格上能画出与△ABC成轴对称，且顶点都在小正方形顶点上的三角形的个数共有4个．
10．抛物线y=-2（x-1）2-3的最大值为（ ）
| A． | -1 | B． | 1 | C． | -3 | D． | 3 |
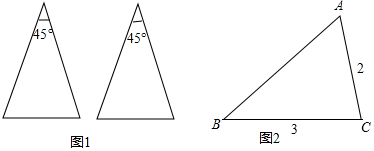
如图，抛物线y=ax2+bx+c（a≠0）与x轴交于A（-4，0），B（2，0），与y轴交于点C（0，2）．