题目内容
如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.
(1)求四边形CEFB的面积;
(2)试判断AF与BE的位置关系,并说明理由;
(3)若∠BEC=15°,求AC的长.
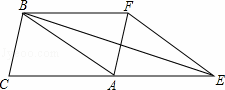
解:(1)由平移的性质得
AF∥BC,且AF=BC,△EFA≌△ABC
∴四边形AFBC为平行四边形
S△EFA=S△BAF=S△ABC=3
∴四边形EFBC的面积为9;
(2)BE⊥AF
证明:由(1)知四边形AFBC为平行四边形
∴BF∥AC,且BF=AC
又∵AE=CA
∴四边形EFBA为平行四边形又已知AB=AC
∴AB=AE
∴平行四边形EFBA为菱形
∴BE⊥AF;
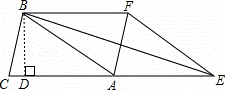
(3)如上图,作BD⊥AC于D
∵∠BEC=15°,AE=AB
∴∠EBA=∠BEC=15°
∴∠BAC=2∠BEC=30°
∴在Rt△BAD中,AB=2BD
设BD=x,则AC=AB=2x
∵S△ABC=3,且S△ABC= AC•BD=
AC•BD= •2x•x=x2
•2x•x=x2
∴x2=3
∵x为正数
∴x=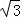
∴AC=2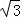 .
.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目




 C沿直线BC方向向右平移到△DEF的位置,AC交DE于点O,连接AD,如果AB=2
C沿直线BC方向向右平移到△DEF的位置,AC交DE于点O,连接AD,如果AB=2 ,BF=6,那么△AOD的面积为 .
,BF=6,那么△AOD的面积为 .