题目内容
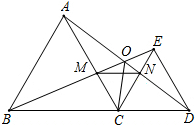 如图,已知△ABC和△CDE都是等边三角形,点B、C、D在同一条直线上,BE交AC于M,AD交CE于N,AD、BE交点O.求证:
如图,已知△ABC和△CDE都是等边三角形,点B、C、D在同一条直线上,BE交AC于M,AD交CE于N,AD、BE交点O.求证:(1)AD=BE;
(2)BM=AN;
(3)△MNC为等边三角形;
(4)MN∥BD;
(5)∠BOD=120°
(6)CO平分∠BOD.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:(1)根据等边三角形的性质得CA=CB,CD=CE,∠ACB=60°,∠DCE=60°,则∠ACE=60°,利用“SAS”可判断△ACD≌△BCE,则AD=BE;
(2)由△ACD≌△BCE得到∠CAD=∠CBE,然后根据“ASA”判断△ACN≌△BCM,所以AN=BM;
(3)由△ACN≌△BCM得到CN=BM,加上∠MCN=60°,则根据等边三角形的判定即可得到△CMN为等边三角形;
(4)由△CMN为等边三角形得到∠CMN=60°,所以∠CMN=∠BCM,于是根据平行线的判定即可得到MN∥BC;
(5)根据三角形内角和定理可得∠CAD+∠CDA=60°,而∠CAD=∠CBE,则∠CBE+∠CDA=60°,然后再利用三角形内角和定理即可得到∠BOD=120°;
(6)作CH⊥BE于H,CQ⊥AD于Q,如图,由△ACD≌△BCE得到CQ=CH,于是根据角平分线的判定定理即可得到CO平分∠BOD.
(2)由△ACD≌△BCE得到∠CAD=∠CBE,然后根据“ASA”判断△ACN≌△BCM,所以AN=BM;
(3)由△ACN≌△BCM得到CN=BM,加上∠MCN=60°,则根据等边三角形的判定即可得到△CMN为等边三角形;
(4)由△CMN为等边三角形得到∠CMN=60°,所以∠CMN=∠BCM,于是根据平行线的判定即可得到MN∥BC;
(5)根据三角形内角和定理可得∠CAD+∠CDA=60°,而∠CAD=∠CBE,则∠CBE+∠CDA=60°,然后再利用三角形内角和定理即可得到∠BOD=120°;
(6)作CH⊥BE于H,CQ⊥AD于Q,如图,由△ACD≌△BCE得到CQ=CH,于是根据角平分线的判定定理即可得到CO平分∠BOD.
解答:证明:(1)∵△ABC和△CDE都是等边三角形,
∴CA=CB,CD=CE,∠ACB=60°,∠DCE=60°,
∴∠ACE=60°,
∴∠ACD=∠BCE=120°,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)∵△ACD≌△BCE,
∴∠CAD=∠CBE,
在△ACN和△BCM中,
,
∴△ACN≌△BCM(ASA),
∴AN=BM;
(3)∵△ACN≌△BCM,
∴CN=BM,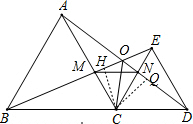
而∠MCN=60°,
∴△CMN为等边三角形;
(4)∵△CMN为等边三角形;
∴∠CMN=60°,
∴∠CMN=∠BCM,
∴MN∥BC;
(5)∵∠CAD+∠CDA=60°,
而∠CAD=∠CBE,
∴∠CBE+∠CDA=60°,
∴∠BOD=120°;
(6)作CH⊥BE于H,CQ⊥AD于Q,如图,
∵△ACD≌△BCE,
∴CQ=CH,
∴CO平分∠BOD.
∴CA=CB,CD=CE,∠ACB=60°,∠DCE=60°,
∴∠ACE=60°,
∴∠ACD=∠BCE=120°,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)∵△ACD≌△BCE,
∴∠CAD=∠CBE,
在△ACN和△BCM中,
|
∴△ACN≌△BCM(ASA),
∴AN=BM;
(3)∵△ACN≌△BCM,
∴CN=BM,

而∠MCN=60°,
∴△CMN为等边三角形;
(4)∵△CMN为等边三角形;
∴∠CMN=60°,
∴∠CMN=∠BCM,
∴MN∥BC;
(5)∵∠CAD+∠CDA=60°,
而∠CAD=∠CBE,
∴∠CBE+∠CDA=60°,
∴∠BOD=120°;
(6)作CH⊥BE于H,CQ⊥AD于Q,如图,
∵△ACD≌△BCE,
∴CQ=CH,
∴CO平分∠BOD.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等边三角形的判定与性质.

练习册系列答案
相关题目
在日历上,如果某月的11日是星期四,那么这个月里下面哪个日期是星期五?( )
| A、4日 | B、19日 |
| C、20日 | D、30日 |
若xn=2,yn=3,则(xy)3n等于( )
| A、12 | B、16 | C、18 | D、216 |
 如图,水坝横断面是梯形ABCD,坝顶宽为3m,坝高4m,斜坡AB长5m,斜坡CD的坡度i=1:1.则坝底AD长为
如图,水坝横断面是梯形ABCD,坝顶宽为3m,坝高4m,斜坡AB长5m,斜坡CD的坡度i=1:1.则坝底AD长为