Question

4．在矩形ABCD中，点E是边CD上任意一点（点E与点C、D不重合），过点A作AF⊥AE，交边CB的延长线于点F，连接EF，与边AB相交于点G．
（1）如果$\frac{AD}{AB}$=1，如图（1），判断△AEF的形状，并说明理由；
（2）如果$\frac{AD}{AB}$=2，如图（2），当点E在边CD上运动时，判断出线段AE、AF之间的数量关系如何变化，并说明理由；
（3）如果AB=3，$\frac{AD}{AB}$=k，当点E在边CD上运动时，是否存在k，使△AEG为等边三角形？若存在，请直接写出k的值以及DE的长度．

Answer 1

分析 （1）由AD：AB=1：1可以得出四边形ABCD是正方形，由其性质就可以得出△ABF≌△ADE，从而得出AF=AE，得出△AEF的形状；
（2）根据条件可以得出△ABF∽△ADE，由相似三角形的性质就可以得出结论；
（3）如图3，当△AEG是等边三角形时，由勾股定理就可以表示出AG、AE、FG，BG的值建立方程求出k值，就可以求出DE的长度．

解答 解：（1）△AEF为等腰直角三角形
理由：如图1，∵AD：AB=1：1，
∴AD=AB．
∵四边形ABCD是矩形，
∴∠D=∠ABF=∠BAD=90°．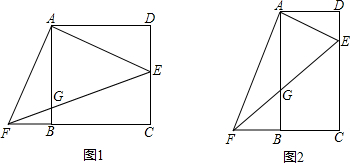
∵AF⊥AE，
∴∠FAE=90°，
∴∠FAE=∠BAD，
∴∠FAE-∠BAE=∠BAD-∠BAE，
即∠BAF=∠DAE．
在△ABF和△DAE中，
$\left\{\begin{array}{l}{∠BAF=∠DAE}\\{AB=AD}\\{∠ABF=∠D}\end{array}\right.$，
∴△ABF≌△ADE，
∴AF=AE，
∴△AEF为等腰直角三角形；

（2）如图2，∵四边形ABCD是矩形，
∴∠D=∠ABF=∠BAD=90°
∵AF⊥AE，
∴∠FAE=90°，
∴∠FAE=∠BAD，
∴△ABF∽△ADE，
∴$\frac{AD}{AB}=\frac{AE}{AF}$．
∵$\frac{AD}{AB}$=$\frac{1}{2}$，
∴$\frac{AE}{AF}$=$\frac{1}{2}$，
即AF=2AE；

（3）∵四边形ABCD是矩形，
∴∠D=∠ABF=∠BAD=90°
∵AF⊥AE，
∴∠FAE=90°．
∵△AEG是等边三角形，
∴AE=AG，∠GAE=∠AEG=60°．
∴∠FAG=∠DAE=∠AFE=30°，
∴AG=FG．
∵AB=3，AD：AB=k，
∴AD=3k．
在Rt△ADE中由勾股定理，得
DE=$\sqrt{3}$k，AE=2$\sqrt{3}$k，
∴AG=FG=2$\sqrt{3}$k，
∴BG=$\sqrt{3}$k．
∵AB=3，
∴GB=3-2$\sqrt{3}$k，
∴$\sqrt{3}$k=3-2$\sqrt{3}$k，
解得：k=$\frac{\sqrt{3}}{3}$，
∴DE=1．

点评 本题考查了矩形的性质的运用，全等三角形的判定及性质的运用，相似三角形的判定及性质的运用，勾股定理的运用，直角三角形的性质的运用，解答时运用勾股定理表示线段的长度是本题的难点．