题目内容
9.在△ABC中,AB=4,BC=a,AC=b,其中a、b是不大于5的自然数,且满足(a+b)(a-b)2=16a-16b,则满足条件且互不全等的三角形共有4个.分析 首先把(a+b)(a-b)2=16a-16b,移项因式分解,得到(a2-b2-16)(a-b)=0,进一步分析探讨得出答案即可.
解答 解:∵(a+b)(a-b)2=16a-16b,
∴(a2-b2-16)(a-b)=0,
∴a2-b2=16,a-b=0,
∴有 4,5,5;4,4,4; 4,3,3;5,4,3共四个.
故答案为:4.
点评 此题考查因式分解的实际运用,三角形的三边关系,利用提取公因式法因式分解和分类探讨是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.若某数的平方根为2a+3和a-15,则这个数是( )
| A. | -18 | B. | $-\frac{2}{3}$ | C. | 121 | D. | 以上结论都不是 |
20.已知数据:10,8,6,10,8,13,11,10,12,7,9,8,12,9,11,12,9,10,11,10,那么频数为4的一组是( )
| A. | 5.5~7.5 | B. | 7.5~9.5 | C. | 9.5~11.5 | D. | 11.5~13.5 |
17.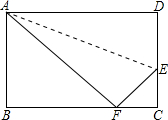 如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )
如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )
 如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )
如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |

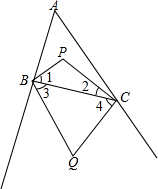 如图,在△ABC中,P是△ABC内角平分线的BP,CP的交点.Q是△ABC中∠B、∠C外角平分线的交点.
如图,在△ABC中,P是△ABC内角平分线的BP,CP的交点.Q是△ABC中∠B、∠C外角平分线的交点.