题目内容
17.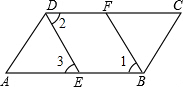 已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC.
已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC.证明:∵BF、DE分别平分∠ABC与∠ADC,(已知)
∴∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ADC角平分线定义
又∵∠ABC=∠ADC ( 已知 )
∴∠1=∠2
又∵∠1=∠3 ( 已知 )
∴∠2=∠3
∴AB∥DC内错角相等,两直线平行.
分析 首先根据角平分线定义可得∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ADC,根据等式的性质可得∠1=∠2,再由条件∠1=∠3可得∠2=∠3,根据内错角相等,两直线平行可得AB∥CD.
解答 证明:∵BF、DE分别平分∠ABC与∠ADC,(已知)
∴∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ADC (角平分线定义)
又∵∠ABC=∠ADC ( 已知 )
∴∠1=∠2,
又∵∠1=∠3 ( 已知 )
∴∠2=∠3
∴AB∥DC (内错角相等,两直线平行),
故答案为:角平分线定义;2;3;内错角相等,两直线平行.
点评 此题主要考查了平行线的判定,关键是掌握内错角相等,两直线平行.

练习册系列答案
相关题目
5.下列说法正确的是( )
| A. | 比-2大8的数是10 | |
| B. | -5<-1<-6 | |
| C. | 数轴上表示数-3的点在原点左边3个单位处 | |
| D. | 100000太大,不能在数轴上表示出来 |
12.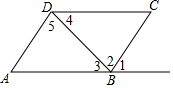 如图,由AD∥BC可以得到的结论是( )
如图,由AD∥BC可以得到的结论是( )
 如图,由AD∥BC可以得到的结论是( )
如图,由AD∥BC可以得到的结论是( )| A. | ∠1=∠2 | B. | ∠1=∠4 | C. | ∠2=∠5 | D. | ∠3=∠4 |
 有一个“三阶幻方”如图所示,字母A、B、C代表的数字分别是2、8、6.
有一个“三阶幻方”如图所示,字母A、B、C代表的数字分别是2、8、6.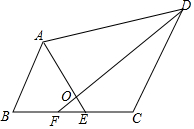 如图,四边形ABCD中,AB∥DC,AE,DF分别是∠BAD,∠ADC的平分线,AE,DF交于点O.
如图,四边形ABCD中,AB∥DC,AE,DF分别是∠BAD,∠ADC的平分线,AE,DF交于点O.
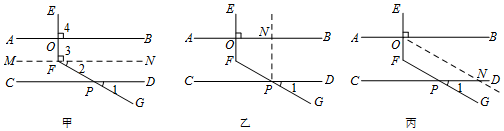

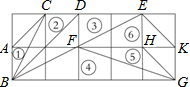 如图所示,在正方形网格上有6个斜三角形,①△ABC,②△BCD,③△BDE,④△BFG,⑤△FGH,⑥△EFK,在②~⑥中,与三角形①相似的有③④⑤(填序号)
如图所示,在正方形网格上有6个斜三角形,①△ABC,②△BCD,③△BDE,④△BFG,⑤△FGH,⑥△EFK,在②~⑥中,与三角形①相似的有③④⑤(填序号)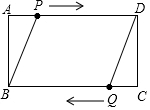 如图,在矩形ABCD中,AB=4cm,AD=6cm,点P从点A出发,以1cm/s的速度沿AD向终点D运动,同时,点Q从点C出发,以1cm/s的速度沿CB向终点B运动,设运动时间为t(s).
如图,在矩形ABCD中,AB=4cm,AD=6cm,点P从点A出发,以1cm/s的速度沿AD向终点D运动,同时,点Q从点C出发,以1cm/s的速度沿CB向终点B运动,设运动时间为t(s).