题目内容
6.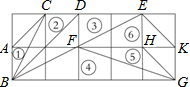 如图所示,在正方形网格上有6个斜三角形,①△ABC,②△BCD,③△BDE,④△BFG,⑤△FGH,⑥△EFK,在②~⑥中,与三角形①相似的有③④⑤(填序号)
如图所示,在正方形网格上有6个斜三角形,①△ABC,②△BCD,③△BDE,④△BFG,⑤△FGH,⑥△EFK,在②~⑥中,与三角形①相似的有③④⑤(填序号)
分析 两三角形三条边对应成比例,两三角形相似,据此即可解答.
解答 解:设每个小正方形的边长为1,则△ABC的各边长分别为1、$\sqrt{2}$、$\sqrt{5}$.则
②△BCD的各边长分别为1、$\sqrt{5}$、2$\sqrt{2}$;
③△BDE的各边长分别为2、2$\sqrt{2}$、2$\sqrt{5}$(为△ABC各边长的2倍);
④△BFG的各边长分别为5、$\sqrt{5}$、$\sqrt{10}$(为△ABC各边长的$\sqrt{5}$倍);
⑤△FGH的各边长分别为2、$\sqrt{2}$、$\sqrt{10}$(为△ABC各边长的$\sqrt{2}$倍);
⑥△EFK的各边长分别为3、$\sqrt{2}$、$\sqrt{5}$.
根据三组对应边的比相等的两个三角形相似得到与三角形①相似的是③④⑤.
故答案为③④⑤.
点评 此题考查了相似三角形的判定,勾股定理,掌握三组对应边的比相等的两个三角形相似是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
1.下列图形中的曲线不表示y与x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
18.一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH折叠,发现GD与GC重合,HF与HE重合.则下列判断正确的是( )
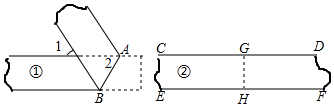

| A. | 纸带①的边线平行,纸带②的边线不平行 | |
| B. | 纸带①的边线不平行,纸带②的边线平行 | |
| C. | 纸带①、②的边线都平行 | |
| D. | 纸带①、②的边线都不平行 |
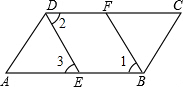 已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC.
已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC.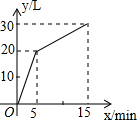 一个装有进水管和出水管的容器,从某时刻开始5min内至进水不出水,在随后的10min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
一个装有进水管和出水管的容器,从某时刻开始5min内至进水不出水,在随后的10min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.