Question

【题目】已知抛物线与轴交于，两点，与轴交于点.

（1）填空： ， .

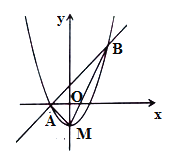
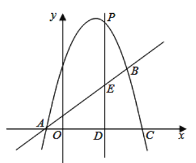
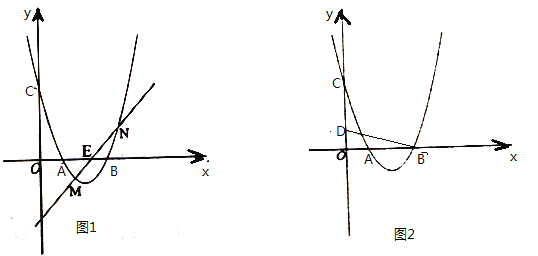
（2）如图1，已知，过点的直线与抛物线交于点、，且点、关于点对称，求直线的解析式.

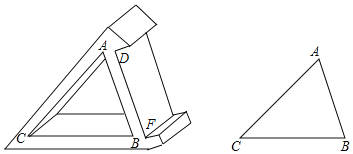
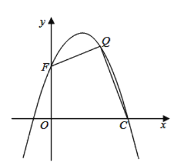
（3）如图2，已知，是第一象限内抛物线上一点，作轴于点，若与相似，请求出点的横坐标.

Answer 1

【答案】（1），;（2）直线;（3）点的横坐标为或

【解析】

（1）把，代入解析式即可求出a,b的值；

（2）设直线MN为y=kx-，根据二次函数联立得到一元二次方程，设交点、的横坐标为x1,x2,根据对称性可得x1+x2=5,根据根与系数的关系求解k，即可求解.

（3）求出OD,OB，设P（x,），得到HP=x,DH=-1=,根据与相似分两种情况列出比例式即可求解.

（1）把，代入

得解得

故答案为：-4；3；

（2）设直线MN为y=kx+b，把代入得b=-

∴直线MN为y=kx-，

联立二次函数得kx-=

整理得x2-(k+4)x++3=0

设交点、的横坐标为x1,x2,

∵点、关于点对称，

∴x1+x2=5

故k+4=5

解得k=1

∴直线；

（3）∵D（0,1），B（3,0）

∴OD=1,OB=3，

设P（x,），

则HP=x,DH=-1=,

当∽时，,即

解得x=

当∽时，,即

解得x=

∴点的横坐标为或.