题目内容
已知,y+2与x成正比例,当x=-2时y=0.
(1)求y与x的函数关系式,
(2)画出函数的图象,观察图象请回答:当x取何值时,y≥0?
(3)设P点在y轴上,(2)中的图象与x轴、y轴分别交于A、B两点,且S△ABP=6,求P点坐标.
(1)求y与x的函数关系式,
(2)画出函数的图象,观察图象请回答:当x取何值时,y≥0?
(3)设P点在y轴上,(2)中的图象与x轴、y轴分别交于A、B两点,且S△ABP=6,求P点坐标.
考点:待定系数法求一次函数解析式,一次函数的图象,一次函数图象上点的坐标特征
专题:
分析:(1)已知y+2与x成正比例,则得到y与x的关系式,代入x和y的值即可求出k的值,进而求出y与x之间的函数关系式;
(2)由“两点确定一条直线”画出图象;
(3)根据三角形的面积公式进行解答.
(2)由“两点确定一条直线”画出图象;
(3)根据三角形的面积公式进行解答.
解答:解:(1)依题意可设y+2=kx(k≠0).则
-2k=2,
解得k=-1.
所以y与x的函数关系式为:y=-x-2;
(2)由(1)知,y=-x-2.
令x=0,则y=-2.
令y=0,则x=-2.
所以,该直线经过点(0,-2),(-2,0).
故图象如图所示:

(3)∵P点在y轴上,
∴设P(0,t).
由(2)知,A(0,-2),B(-2,0).
则S△ABP=
BP•OA=
|t+2|×2=6,
解得t=4或t=-8.
故P(0,4)或(0,-8).
-2k=2,
解得k=-1.
所以y与x的函数关系式为:y=-x-2;
(2)由(1)知,y=-x-2.
令x=0,则y=-2.
令y=0,则x=-2.
所以,该直线经过点(0,-2),(-2,0).
故图象如图所示:

(3)∵P点在y轴上,
∴设P(0,t).
由(2)知,A(0,-2),B(-2,0).
则S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
解得t=4或t=-8.
故P(0,4)或(0,-8).
点评:本题考查了待定系数法求一次函数解析式,一次函数图象,一次函数图象上点的坐标特征.解答(3)题时,一定要细心运算,点P的位置应该有2个.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
在平面直角坐标系中,将点A向右平移2个单位长度后得到点A′(3,2),则点A的坐标是( )
| A、(3,4) |
| B、(3,0) |
| C、(1,2) |
| D、(5,2) |
 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点出发沿AB边 向B以1cm/s的速度移动,点Q从B点出发沿BC向C点以2cm/s的速度移动,当其中一个点到达终点时两个点同时停止运动,在两个点运动过程中,请回答:
如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点出发沿AB边 向B以1cm/s的速度移动,点Q从B点出发沿BC向C点以2cm/s的速度移动,当其中一个点到达终点时两个点同时停止运动,在两个点运动过程中,请回答:
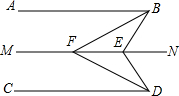 如图,直线AB∥MN∥CD,E,F为直线MN上的两点,BF平分∠ABE,DF平分∠CDE,∠BED=120°,求∠BFD的度数.
如图,直线AB∥MN∥CD,E,F为直线MN上的两点,BF平分∠ABE,DF平分∠CDE,∠BED=120°,求∠BFD的度数. 已知:如图,AB∥CD,∠A+∠D=180°,求证:AC∥DE.
已知:如图,AB∥CD,∠A+∠D=180°,求证:AC∥DE.