题目内容
2.甲、乙两个不透明的口袋,甲口袋中装有2个分别标有数字1,-1的小球,乙口袋中装有3个分别标有数字-1,0,1的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字为x,再从乙口袋中摸出一个小球记下数字为y.(1)请用列表或树状图的方法(只选其中一种),表示出点P可能出现的所有坐标;
(2)求点P(x,y)在函数y=-x图象上方的概率.
分析 (1)画树状图展示所有6种等可能的结果数;
(2)根据直线上的点的坐标特征可判断在函数y=-x图象上方的点有(1,1)和(1,0),然后根据概率公式求解.
解答 解:(1)画树状图为:
共有6种等可能的结果数,它们为(1,1),(1,0),(1,-1),(-1,1),(-1,0),(-1,-1);
(2)在函数y=-x图象上方的点有(1,1)和(1,0),
所以点P(x,y)在函数y=-x图象上方的概率=$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.

练习册系列答案
相关题目
17.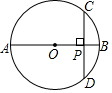 ⊙O的直径AB=10cm,弦CD⊥AB,垂足为P.若OP:OB=3:5,则CD的长为( )
⊙O的直径AB=10cm,弦CD⊥AB,垂足为P.若OP:OB=3:5,则CD的长为( )
 ⊙O的直径AB=10cm,弦CD⊥AB,垂足为P.若OP:OB=3:5,则CD的长为( )
⊙O的直径AB=10cm,弦CD⊥AB,垂足为P.若OP:OB=3:5,则CD的长为( )| A. | 6cm | B. | 4cm | C. | 8cm | D. | $\sqrt{91}$cm |
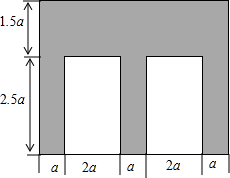 某公园中一块草坪的形状如图中的阴影部分.
某公园中一块草坪的形状如图中的阴影部分.