题目内容
△ABC中,射线AD平分∠BAC,AD交边BC于E点.
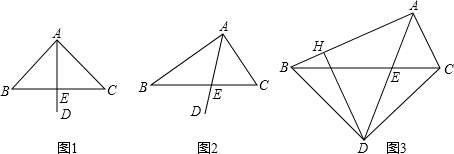
(1)如图1,若AB=AC,∠BAC=90°,则 ( )
( ) ;
;

(2)如图2,若AB≠AC,则(1)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由;

(3)如图3,若AB>AC,∠BAC=∠BDC=90°,∠ABD为锐角,DH⊥AB于H,则线段AB、AC、BH之间的数量关系是( ),并证明.

【答案】
(1)=;(2)成立,证明见解析;(3)  ,证明见解析.
,证明见解析.
【解析】
试题分析:
由 ,
, 平分
平分 ,根据等腰三角形“三线合一”可得:
,根据等腰三角形“三线合一”可得: .所以
.所以 .
.
(2)求 与
与 、
、 与
与 的比,由图可知.四条线段均为
的比,由图可知.四条线段均为 和
和 的两边,可用两三角形的两组边与高分别表示面积.如图,过点
的两边,可用两三角形的两组边与高分别表示面积.如图,过点 分别作
分别作 于点
于点 ,
, 于点
于点 ,过点
,过点 作
作 于点
于点 ,由
,由 平分
平分 可得
可得 ;然后根据面积公式可得:
;然后根据面积公式可得:
 ;
; .所以
.所以 .故图(1)中的结论成立.
.故图(1)中的结论成立.
(3)如图,过点 作
作 交
交 的延长线于点
的延长线于点 ,此时易证
,此时易证 得
得 ,因为
,因为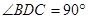 ,由同角
,由同角 的余角相等,得
的余角相等,得 .进而由
.进而由 可证
可证 ,得
,得 ;此时应考虑将等式
;此时应考虑将等式 转化为用
转化为用 、
、 、
、 来表示,即
来表示,即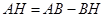 ,
, ;所以
;所以 ,移项可得
,移项可得 .
.
试题解析:(1)解:∵
 平分
平分
∴
∴
(2)图(1)中的结论成立.
证明:如图,过点 分别作
分别作 于点
于点 ,
, 于点
于点 ,过点
,过点 作
作 于点
于点 ,
,
∵ 平分
平分
∴
根据面积公式可得 ,
, ;
;
所以 .故图(1)中的结论成立.
.故图(1)中的结论成立.

(3)证明:如图,过点 作
作 交
交 的延长线于
的延长线于
∵ 平分
平分 ,
, ,
,
∴
∵在 和
和 中
中
 .
.
∴
∴
∵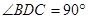
∴
又∵
∴
∴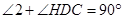
∴
在 和
和 中
中

∴
∴
∵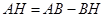

∴
∴

考点:1、角平分线的性质.2、三角形的面积公式的灵活运用.3、三角形全等的判定.4、正方形的判定及性质

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目