题目内容
△ABC中,射线AD平分∠BAC,AD交边BC于E点.
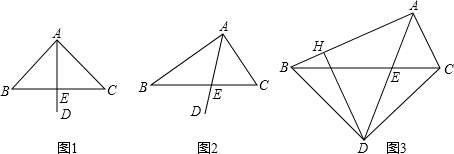
(1)如图1,若AB=AC,∠BAC=90°,则
;
(2)如图2,若AB≠AC,则(1)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由;
(3)如图3,若AB>AC,∠BAC=∠BDC=90°,∠ABD为锐角,DH⊥AB于H,则线段AB、AC、BH之间的数量关系是 ,并证明.

(1)如图1,若AB=AC,∠BAC=90°,则
| AB |
| AC |
| BE |
| EC |
(2)如图2,若AB≠AC,则(1)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由;
(3)如图3,若AB>AC,∠BAC=∠BDC=90°,∠ABD为锐角,DH⊥AB于H,则线段AB、AC、BH之间的数量关系是
分析:(1)根据等腰三角形的在可以直接得出
=
;
(2)作EH⊥AB于H,EQ⊥AC于Q,AN⊥BC于N,根据角平分线的性质可以得出EH=EQ,由三角形的面积相等就可以求出结论;
(3)作DQ⊥AC交AC的延长线于Q,则DH=DQ,证△AHD≌△AQD,得AH=AQ,再证△DHB≌△DQC,得BH=CQ,有AB-BH=AC+CQ(BH),AB-AC=2BH.
| AB |
| AC |
| BE |
| EC |
(2)作EH⊥AB于H,EQ⊥AC于Q,AN⊥BC于N,根据角平分线的性质可以得出EH=EQ,由三角形的面积相等就可以求出结论;
(3)作DQ⊥AC交AC的延长线于Q,则DH=DQ,证△AHD≌△AQD,得AH=AQ,再证△DHB≌△DQC,得BH=CQ,有AB-BH=AC+CQ(BH),AB-AC=2BH.
解答:解:(1)∵AB=AC,AD平分∠BAC,
∴BE=CE.
∴
=1.
∵AB=AC,
∴
=1,
∴
=
.
故答案为:=;
(2)成立,
证明:作EH⊥AB于H,EQ⊥AC于Q,AN⊥BC于N,则EH=EQ,设AB=c,AC=b,BE=m,EC=n,EH=h1,AN=h2,
∵S△ABE:S△AEC=
h1c÷
h1b=c:b,S△ABE:S△AEC=
h2m÷
h2n=m:n,
∴c:b=m:n,
即
=
;
(3)AB-AC=2BH.
理由:作DQ⊥AC交AC的延长线于Q,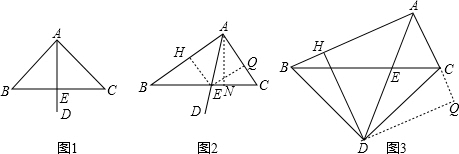
∴∠Q=90°
∵DH⊥AB,AD平分∠BAC,
∴DH=DQ,∠AHD=90°,∠HAD=∠CAD.
∴∠AHD=∠Q.
在△AHD和△AQD中,
,
∴△AHD≌△AQD(AAS),
∴AH=AQ.
∵∠BAC=90°,∠AHD=∠Q=90°,
∴四边形AHDQ是矩形,
∴∠HDQ=90°.
∵∠BDC=90°,
∴∠HDQ=∠BDC,
∴∠HDQ-∠HDC=∠BDC=∠HDC,
∴∠CDQ=∠BDH.
在△DHB和△DQC中
∴△DHB≌△DQC(AAS),
∴BH=CQ,
∵AB-BH=AH,
∴AB-BH=AQ,
∴AB-BH=AC+CQ,
∴AB-AC=2BH.
故答案为:AB-AC=2BH.
∴BE=CE.
∴
| BE |
| CE |
∵AB=AC,
∴
| AB |
| AC |
∴
| AB |
| AC |
| BE |
| EC |
故答案为:=;
(2)成立,
证明:作EH⊥AB于H,EQ⊥AC于Q,AN⊥BC于N,则EH=EQ,设AB=c,AC=b,BE=m,EC=n,EH=h1,AN=h2,
∵S△ABE:S△AEC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴c:b=m:n,
即
| AB |
| AC |
| BE |
| EC |
(3)AB-AC=2BH.
理由:作DQ⊥AC交AC的延长线于Q,

∴∠Q=90°
∵DH⊥AB,AD平分∠BAC,
∴DH=DQ,∠AHD=90°,∠HAD=∠CAD.
∴∠AHD=∠Q.
在△AHD和△AQD中,
|
∴△AHD≌△AQD(AAS),
∴AH=AQ.
∵∠BAC=90°,∠AHD=∠Q=90°,
∴四边形AHDQ是矩形,
∴∠HDQ=90°.
∵∠BDC=90°,
∴∠HDQ=∠BDC,
∴∠HDQ-∠HDC=∠BDC=∠HDC,
∴∠CDQ=∠BDH.
在△DHB和△DQC中
|
∴△DHB≌△DQC(AAS),
∴BH=CQ,
∵AB-BH=AH,
∴AB-BH=AQ,
∴AB-BH=AC+CQ,
∴AB-AC=2BH.
故答案为:AB-AC=2BH.
点评:本题考查了等腰三角形的性质的运用,角平分线的性质的运用,等式的性质的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
 ( )
( ) ;
;

