题目内容
 已知:将Rt△ABC沿着BC方向平移BE距离得到Rt△DEF,AB=8,BE=5,DH=2.
已知:将Rt△ABC沿着BC方向平移BE距离得到Rt△DEF,AB=8,BE=5,DH=2.(1)直接填空:CF=
(2)试说明:四边形CHDF与四边形ABEH的面积相等;
(3)求四边形CHDF的面积.
考点:平移的性质
专题:
分析:(1)根据平移距离等于对应顶点之间的距离可得CF=BE;
(2)根据平移变化只改变图形的位置不改变图形的形状可得S△ABC=S△DEF,然后求解即可;
(3)表示出HE,再求出梯形ABEH的面积,即为四边形CHDF的面积.
(2)根据平移变化只改变图形的位置不改变图形的形状可得S△ABC=S△DEF,然后求解即可;
(3)表示出HE,再求出梯形ABEH的面积,即为四边形CHDF的面积.
解答:解:(1)∵Rt△ABC沿着BC方向平移BE距离得到Rt△DEF,BE=5,
∴CF=BE=5;
(2)由平移的性质得,S△ABC=S△DEF,
∴S△ABC-S△CEH=S△DEF-S△CEH,
即,四边形CHDF与四边形ABEH的面积相等;
(3)∵AB=8,DH=2,
∴HE=8-2=6,
∴梯形ABEH的面积=
(6+8)×5=35,
∴四边形CHDF的面积是35.
∴CF=BE=5;
(2)由平移的性质得,S△ABC=S△DEF,
∴S△ABC-S△CEH=S△DEF-S△CEH,
即,四边形CHDF与四边形ABEH的面积相等;
(3)∵AB=8,DH=2,
∴HE=8-2=6,
∴梯形ABEH的面积=
| 1 |
| 2 |
∴四边形CHDF的面积是35.
点评:本题考查了平移的性质,熟记平移变化只改变图形的位置不改变图形的形状是解题的关键.

练习册系列答案
相关题目
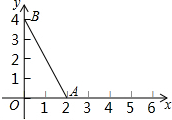 △OAB的三个顶点坐标分别是O(0,0),A(2,0),B(0,4).
△OAB的三个顶点坐标分别是O(0,0),A(2,0),B(0,4).
 在直角坐标系中,△ABC的三个顶点的位置如图所示,现将△ABC沿AA′的方向平移,使得点A移至图中的点A′的位置.
在直角坐标系中,△ABC的三个顶点的位置如图所示,现将△ABC沿AA′的方向平移,使得点A移至图中的点A′的位置.