题目内容
14.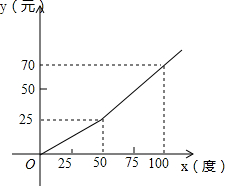 为了缓解用电紧张矛盾,某电力公司特别制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
为了缓解用电紧张矛盾,某电力公司特别制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.(1)根据图象,请分别写出当0≤x≤50和x>50,y关于x的函数关系式;
(2)当每月用电量为35度时,应缴电费多少元?
(3)当每月用电量为110度时,应缴电费多少元?
分析 (1)0≤x≤50时,函数为正比例函数,把(50,25)代入正比例函数解析式即可.x>50时,为一次函数解析式,把(50,25),(100,70)代入即可求得;
(2)把x=35代入y=$\frac{1}{2}$x,即可解答;
(3)把x=110代入y=0.9x-20,即可解答.
解答 解:(1)①当月用电量0≤x≤50时,y是x的正比例函数,
设y=k1x,
∵当x=50时,y=25,
∴25=50k1,
∴${k}_{1}=\frac{1}{2}$
∴y=$\frac{1}{2}$x.
②当月用电量x>50时,y是x的一次函数,
设y=k2x+b,∵当x=50时,y=25;当x=100时,y=70,
∴$\left\{\begin{array}{l}{50{k}_{2}+b=25}\\{100{k}_{2}+b=70}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{k}_{2}=0.9}\\{b=-20}\end{array}\right.$,
∴y=0.9x-20;
(2)把x=35代入y=$\frac{1}{2}$x,得:y=17.5,
答:当每月用电量为35度时,应缴电费17.5元;
(3)把x=110代入y=0.9x-20,得:y=99-20=79,
答:当每月用电量为110度时,应缴电费79元.
点评 本题考查了一次函数的应用,图中的函数为分段函数,注意自变量的取值范围相对应的函数值.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
9.某汽车出租公司有120辆车出租,通过市场调查获得下列信息(如表):
(1)从市场调查获得的信息知,每日能出租汽车数y(辆)与每辆车的日租金数x(元)满足一函数关系(填“一次、二次、反比例”):函数关系式为y=-0.2x+140;
(2)请在表格最下一行,填写该公司出租汽车后所获得相应的日收入;
(3)按照上述规律,根据你所学的函数知识帮该公司解答:每辆车租车的日租金定为多少时,才能使公司的日收入获得最多?
| 每辆车的日租金x(元) | 200 | 220 | 240 | 270 | 300 | … |
| 日出租汽车数y(辆) | 100 | 96 | 92 | 86 | 80 | … |
| 出租汽车后的日收入(元) | 20000 | 21120 | 22080 | 23220 | 24000 |
(2)请在表格最下一行,填写该公司出租汽车后所获得相应的日收入;
(3)按照上述规律,根据你所学的函数知识帮该公司解答:每辆车租车的日租金定为多少时,才能使公司的日收入获得最多?
4.在△ABC中,AC=BC=4,∠ACB=90°,D是AC边的中点,E是AB边上一动点,连结EC,ED,则EC+ED的最小值是( )
| A. | 2$\sqrt{10}$ | B. | $\sqrt{10}$ | C. | 2$\sqrt{5}$ | D. | $\sqrt{5}$ |

 如图已知△ABC,请你用三角尺和量角器作图,作△ABC的:①中线AD;②角平分线BE;③高CH.
如图已知△ABC,请你用三角尺和量角器作图,作△ABC的:①中线AD;②角平分线BE;③高CH. 如图,已知函数y=2x-5,观察图象回答下列问题
如图,已知函数y=2x-5,观察图象回答下列问题