题目内容
6.矩形的两条对角线的夹角为60°,较短的边长为1cm,则矩形的面积为$\sqrt{3}$cm2.分析 由矩形的性质得出OA=OB,再证明△AOB是等边三角形,得出OA=AB=1cm,由勾股定理求出BC,即可得出结果.
解答 解:如图所示: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
又∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=AB=1cm,
∴AC=2OA=2cm,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴矩形ABCD的面积=AB•BC=1×$\sqrt{3}$=$\sqrt{3}$(cm2);
故答案为:$\sqrt{3}$.
点评 本题考查了矩形的性质、等边三角形的判定与性质、勾股定理;熟练掌握矩形的性质,由勾股定理求出BC是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列各角不是多边形的内角的是( )
| A. | 180° | B. | 540° | C. | 1900° | D. | 1080° |
16.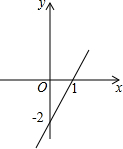 如图,已知一次函数y=kx+b(k、b为常数,k≠0)的图象,当y>-2时,x的取值范围为( )
如图,已知一次函数y=kx+b(k、b为常数,k≠0)的图象,当y>-2时,x的取值范围为( )
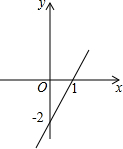 如图,已知一次函数y=kx+b(k、b为常数,k≠0)的图象,当y>-2时,x的取值范围为( )
如图,已知一次函数y=kx+b(k、b为常数,k≠0)的图象,当y>-2时,x的取值范围为( )| A. | x<1 | B. | x>1 | C. | x<0 | D. | x>0 |
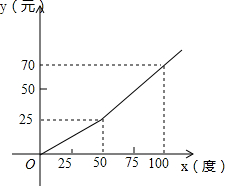 为了缓解用电紧张矛盾,某电力公司特别制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
为了缓解用电紧张矛盾,某电力公司特别制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示. 小明家有一块三角形菜地,要种面积相等的四种蔬菜,请你设计两种方案,把这块地分成四块面积相等的三角形地块分别种植这四种蔬菜.
小明家有一块三角形菜地,要种面积相等的四种蔬菜,请你设计两种方案,把这块地分成四块面积相等的三角形地块分别种植这四种蔬菜. 请把下面的小船图案先向上平移3格,再向右平移4格.
请把下面的小船图案先向上平移3格,再向右平移4格.