题目内容
1. 如图,Rt△AOB的顶点A在双曲线y=$\frac{m}{x}$上,且S△AOB=3,求m的值.
如图,Rt△AOB的顶点A在双曲线y=$\frac{m}{x}$上,且S△AOB=3,求m的值.
分析 根据反比例函数的系数m的几何意义:在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|m|,且保持不变,可得$\frac{1}{2}$|m|=S△AOB=3,据此求出m的值是多少即可.
解答 解:∵△AOB的面积是3,
∴$\frac{1}{2}$|m|=3,
∴|m|=6,
解得k=±6,
又∵双曲线y=$\frac{m}{x}$的图象经过第二、四象限,
∴m=-6,
即k的值是-6.
点评 本题主要考查了反比例函数的系数k的几何意义,要熟练掌握,解答此题的关键是要明确:比例系数k的几何意义在反比例函数y=xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.化简:(a-b)$\sqrt{-\frac{1}{a-b}}$的结果是( )
| A. | $\sqrt{a-b}$ | B. | $\sqrt{-a-b}$ | C. | -$\sqrt{a-b}$ | D. | -$\sqrt{b-a}$ |
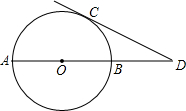 如图,AB是⊙O的直径,过点C的切线交AB的延长线于点D.若∠ADC=30°,BD=10,求⊙O的半径.
如图,AB是⊙O的直径,过点C的切线交AB的延长线于点D.若∠ADC=30°,BD=10,求⊙O的半径. 已知如图,点C,D在线段AB上,PC=PD.请你添加一个条件,使图中存在全等三角形并给予证明.
已知如图,点C,D在线段AB上,PC=PD.请你添加一个条件,使图中存在全等三角形并给予证明.