题目内容
若m,n互为相反数,x,y互为倒数,则(m+n)+5xy的值为( )
| A、5 | B、-5 |
| C、0 | D、以上答案都不对 |
考点:代数式求值,相反数,倒数
专题:
分析:根据互为相反数的两个数的和等于0可得m+n=0,互为倒数的两个数的乘积是1可得xy=1,然后代入代数式进行计算即可得解.
解答:解:∵m,n互为相反数,
∴m+n=0,
∵x,y互为倒数,
∴xy=1,
∴(m+n)+5xy=0+5×1=5.
故选A.
∴m+n=0,
∵x,y互为倒数,
∴xy=1,
∴(m+n)+5xy=0+5×1=5.
故选A.
点评:本题考查了代数式求值,主要利用了相反数的定义和倒数的定义,是基础题,熟记概念是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在一个不透明的布袋中装有红色、白色玻璃球共60个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在25%左右,则口袋中红色球可能有( )
| A、5个 | B、10个 |
| C、15个 | D、45个 |
若关于x的方程2(
-k)x-3x=-1无解,则( )
| 1 |
| 2 |
| A、k=-1 | B、k=l |
| C、k≠-1 | D、k≠1 |
若将一函数的图象向右平行移动2个单位,再向上平移2个单位,可得到的抛物线y=2x2,则原函数解析式是( )
| A、y=2(x+2)2-2 |
| B、y=2(x+2)2+2 |
| C、y=2(x-2)2-2 |
| D、y=2(x-2)2+2 |
已知x=0是二次方程(m+1)x2+mx+4m2-4=0的一个解,那么m的值是( )
| A、0 | B、1 | C、-1 | D、±1 |
 如图,在△ABC中,∠ACB=90°,∠BAC=30°,在直线BC或AC上取一点P,使得△PAB为等腰三角形,这样的点P共有
如图,在△ABC中,∠ACB=90°,∠BAC=30°,在直线BC或AC上取一点P,使得△PAB为等腰三角形,这样的点P共有



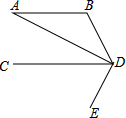 如图,已知AB∥CD,DA平分∠BDC,DE⊥AD于D,∠B=110°,求∠BDE的度数.
如图,已知AB∥CD,DA平分∠BDC,DE⊥AD于D,∠B=110°,求∠BDE的度数.