题目内容
19.解方程:(1)x2-2x-2=0;
(2)(y+2)2=(3y-1)2.
分析 (1)利用配方法解方程;
(2)先移项得到(y+2)2-(3y-1)2=0,然后利用因式分解法解方程.
解答 解:(1)x2-2x+1=3,
(x-1)2=3,
x-1=±$\sqrt{3}$,
所以x1=1+$\sqrt{3}$,x2=1-$\sqrt{3}$;
(2)(y+2)2-(3y-1)2=0,
(y+2+3y-1)(y+2-3y+1)=0,
y+2+3y-1=0或y+2-3y+1=0,
所以y1=-$\frac{1}{4}$,y2=$\frac{3}{2}$.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
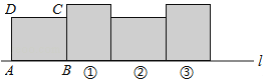 在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2016次后,顶点A在整个旋转过程中所经过的路程之和是3024π.
在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2016次后,顶点A在整个旋转过程中所经过的路程之和是3024π. 已知二次函数y=2x2-4x-6.
已知二次函数y=2x2-4x-6. 如图,⊙O的半径为2,点O到直线l的距离为4,过l上任一点P作⊙O的切线,切点为Q;若以PQ为边作正方形PQRS,则正方形PQRS的面积最小值为12.
如图,⊙O的半径为2,点O到直线l的距离为4,过l上任一点P作⊙O的切线,切点为Q;若以PQ为边作正方形PQRS,则正方形PQRS的面积最小值为12.