题目内容
18.(1)计算:|1-$\sqrt{3}$|-$\sqrt{(-2)^{2}}$+$\sqrt{2\frac{1}{4}}$.(2)求x的值:4(x+1)2-9=0.
分析 (1)原式利用绝对值的代数意义,二次根式性质计算即可得到结果;
(2)方程整理后,开方即可求出x的值.
解答 解:(1)原式=$\sqrt{3}$-1-2+$\frac{3}{2}$=$\sqrt{3}$-$\frac{3}{2}$;
(2)方程整理得:(x+1)2=$\frac{9}{4}$,
开方得:x+1=±$\frac{3}{2}$,
解得:x=$\frac{1}{2}$或x=-$\frac{5}{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
13.在代数式:$\frac{1}{2}$x-y,-$\frac{5}{y}$,a,x2-y+$\frac{2}{3}$,$\frac{x-y}{3}$中,单项式有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.计算 $\frac{{x}^{2}-5x+6}{{x}^{2}-1}$÷$\frac{x-3}{{x}^{2}+x}$的结果是( )
| A. | $\frac{x(x-1)}{x-2}$ | B. | $\frac{x(x-2)}{x-1}$ | C. | $\frac{x-2}{x(x-1)}$ | D. | $\frac{x-1}{x(x-2)}$ |
8.方程x2-1=2x化为一元二次方程的一般形式后,二次项系数为1,一次项系数、常数项分别是( )
| A. | -1、-2 | B. | -2、-1 | C. | 2、-1 | D. | -1、2 |
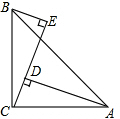 如图,△ABC中,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,垂足分别为E和D.试猜想线段AD、BE、DE三者之间有何数量关系?并证明你的猜想.
如图,△ABC中,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,垂足分别为E和D.试猜想线段AD、BE、DE三者之间有何数量关系?并证明你的猜想.