题目内容
在Rt△ABC中，已知两边长为3、4，则第三边的长为 ．
考点：勾股定理
专题：分类讨论
分析：分两种情况考虑：若4为直角边，可得出3也为直角边，第三边为斜边，利用勾股定理求出斜边，即为第三边；若4为斜边，可得3和第三边都为直角边，利用勾股定理即可求出第三边．
解答：解：若4为直角边，可得3为直角边，第三边为斜边，根据勾股定理得第三边为
=5；
若4为斜边，3和第三边都为直角边，根据勾股定理得第三边为
=
，
则第三边长为5或．
故答案为：5或
．
| 32+42 |
若4为斜边，3和第三边都为直角边，根据勾股定理得第三边为
| 42-32 |
| 7 |
则第三边长为5或．
故答案为：5或
| 7 |
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
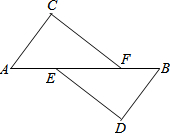已知，如图：A、E、F、B在一条直线上，AE=BF，∠C=∠D，AC∥BD，