题目内容
Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，则它的外心与直角顶点的距离是为（ ）
| A、2cm | B、2.5cm |
| C、3cm | D、4cm |
考点：三角形的外接圆与外心
专题：计算题
分析：先利用勾股定理计算出AB=5cm，再利用直角三角形的外心为斜边的中点得到外接圆的半径为2.5cm，于是得到它的外心与直角顶点的距离．
解答：解：Rt△ABC中，∵∠C=90°，AC=3cm，BC=4cm，
∴AB=
=5cm，
∴Rt△ABC为外接圆的直径为5cm，
即△ABC的外心为AB的中点，
∴它的外心与直角顶点的距离是
cm．
故选B．
∴AB=
| AC2+BC2 |
∴Rt△ABC为外接圆的直径为5cm，
即△ABC的外心为AB的中点，
∴它的外心与直角顶点的距离是
| 5 |
| 2 |
故选B．
点评：本题考查了三角形的外接圆与外心：经过三角形的三个顶点的圆，叫做三角形的外接圆．三角形外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心．掌握直角三角形的外心为斜边的中点是解题的关键．
练习册系列答案
相关题目
据统计，2014年我国用义务教育经费支持了13940000名农民工随迁子女在城市里接受义务教育，这个数字精确到百万位后用科学记数法可表示为（ ）
| A、1.39×107 |
| B、1.4×107 |
| C、1.40×107 |
| D、13.94×107 |
如图，△ABC三个顶点的坐标分别为A（-3，-1）、B（-4，-3）、C（-2，-5）．
如图，C，D是线段AB上的两点，E是AC的中点，F是BD是中点，若EF=a，CD=b，则AB的长（ ）| A、a-b | B、a+b |
| C、2a-b | D、2a+b |
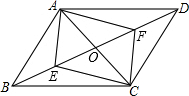如图，在平行四边形ABCD中AC，BD相交于点O，E，F分别是OB、OD的中点．