题目内容
6．
小明作业本上画的三角形被墨迹污染了，他想画出一个与原来完全一样的三角形，他该怎么办呢？请你帮助他想出一个办法来，并说明你的理由．
分析 根据图象，三角形有两角和它们的夹边是完整的，所以可以根据“角边角”画出．
解答 
解：根据题意，三角形的两角和它们的夹边是完整的，
所以可以利用“角边角”定理作出完全一样的三角形．
点评 此题主要考查了全等三角形的应用，熟练掌握全等三角形的判定方法是解题关键．
练习册系列答案
相关题目
16．
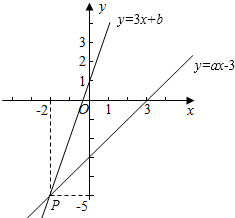如图，已知函数y=3x+b和y=ax-3的图象交于点P（-2，-5），则根据图象可得不等式3x+b＞ax-3的解集是（ ）
如图，已知函数y=3x+b和y=ax-3的图象交于点P（-2，-5），则根据图象可得不等式3x+b＞ax-3的解集是（ ）| A． | x＞-2 | B． | x＜-2 | C． | -2＜x＜0 | D． | x＞0 |
17．
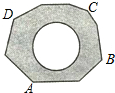如图，地面上有一个不规则的封闭图形ABCD，为求得它的面积，小明在此封闭图形内画出一个半径为1米的圆后，在附近闭上眼睛向封闭图形内掷小石子（可把小石子近似地看成点），记录如下：
（1）当投掷的次数很大时，则m：n的值越来越接近0.5；
（2）若以小石子所落的有效区域为总数（即m+n），则随着投掷次数的增大，小石子落在圆内（含圆上）的频率值稳定在$\frac{1}{3}$；
（3）请你利用（2）中所得频率的值，估计整个封闭图形ABCD的面积是3π米2（结果保留π）
如图，地面上有一个不规则的封闭图形ABCD，为求得它的面积，小明在此封闭图形内画出一个半径为1米的圆后，在附近闭上眼睛向封闭图形内掷小石子（可把小石子近似地看成点），记录如下： | 50 | 50 | 300 | … |
| 石子落在圆内（含圆上）次数m | 14 | 48 | 89 | … |
| 石子落在圆以外的阴影部分（含外缘上）次数n | 30 | 95 | 180 | … |
（2）若以小石子所落的有效区域为总数（即m+n），则随着投掷次数的增大，小石子落在圆内（含圆上）的频率值稳定在$\frac{1}{3}$；
（3）请你利用（2）中所得频率的值，估计整个封闭图形ABCD的面积是3π米2（结果保留π）
14．在△ABC中，AB=2，AC=3，$\overrightarrow{AB}$•$\overrightarrow{BC}$=1，则BC=（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{7}$ | C． | 2$\sqrt{2}$ | D． | $\sqrt{23}$ |
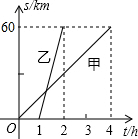A，B两地相距60km．甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶，由A地到达B地，他们行驶的路程s（km）与甲出发后的时间t（h）之间的函数图象如图所示
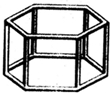一个六棱柱模型如图所示，它的底面边长都是5cm，侧棱长4cm，观察这个模型，回答下列问题：
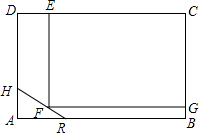为实现城市绿化，某房地产公司要在拆迁地矩形ABCD（如图）上规划出一块矩形公园CEFG，但不能超过文物保护区△AHR的红线HR．已知AB=210cm，AD=140cm，AR=60cm，AH=40cm，那么当边CE多长时才能使公园CEFG占地面积最大？并求出最大面积．