题目内容
已知一元二次方程x2+px+q+2=0的一根为3.
(1)求q关于p的关系式;
(2)求证:抛物线y=x2+px+q与x轴有两个交点;
(3)设抛物线y=x2+px+q与x轴相交于A(x1,0)、B(x2,0)两点,且x1+x2-5x1x2+1=0,求抛物线的解析式.
(1)求q关于p的关系式;
(2)求证:抛物线y=x2+px+q与x轴有两个交点;
(3)设抛物线y=x2+px+q与x轴相交于A(x1,0)、B(x2,0)两点,且x1+x2-5x1x2+1=0,求抛物线的解析式.
考点:抛物线与x轴的交点,根与系数的关系
专题:计算题
分析:(1)由一元二次方程的一根为3,将x=3代入方程得到p与q的关系式;
(2)表示出方程根的判别式,将(1)得出关系式代入,配方后根据完全平方式大于等于0即可得证;
(3)利用根与系数的关系表示出x1+x2=-p,x1x2=q,代入已知等式得到关系式,与(1)的关系式联立求出p与q的值,即可确定出抛物线解析式.
(2)表示出方程根的判别式,将(1)得出关系式代入,配方后根据完全平方式大于等于0即可得证;
(3)利用根与系数的关系表示出x1+x2=-p,x1x2=q,代入已知等式得到关系式,与(1)的关系式联立求出p与q的值,即可确定出抛物线解析式.
解答:(1)解:把x=3代入得32+3p+q+2=0,
∴q=-3p-11;
(2)证明:∵一元二次方程x2+px+q=0的判别式△=p2-4q,
由(1)得q=-3p-11,
∴△=p2+4(3p+11)=p2+12p+44=(p+6)2+8>0,
∴一元二次方程x2+px+q=0有两个不相等的实根,
∴抛物线y=x2+px+q与x轴有两个交点;
(3)解:∵x1,x2是方程x2+px+q=0的两个根,
∴x1+x2=-p,x1x2=q,
∵x1+x2-5x1x2+1=0,
∴-p-5q+1=0,
由(1)得q=-3p-11,
解得
,
∴抛物线的解析式为y=x2-4x+1.
∴q=-3p-11;
(2)证明:∵一元二次方程x2+px+q=0的判别式△=p2-4q,
由(1)得q=-3p-11,
∴△=p2+4(3p+11)=p2+12p+44=(p+6)2+8>0,
∴一元二次方程x2+px+q=0有两个不相等的实根,
∴抛物线y=x2+px+q与x轴有两个交点;
(3)解:∵x1,x2是方程x2+px+q=0的两个根,
∴x1+x2=-p,x1x2=q,
∵x1+x2-5x1x2+1=0,
∴-p-5q+1=0,
由(1)得q=-3p-11,
解得
|
∴抛物线的解析式为y=x2-4x+1.
点评:此题考查了抛物线与x轴的交点,根与系数的关系式,以及根的判别式,弄清题意是解本题的关键.

练习册系列答案
相关题目
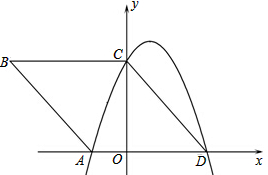 如图,在直角坐标系中,菱形ABCD的顶点A、C、D在坐标轴上,二次函数
如图,在直角坐标系中,菱形ABCD的顶点A、C、D在坐标轴上,二次函数
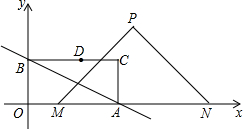 如图,在平面直角坐标系中,直线
如图,在平面直角坐标系中,直线
 如图,甲乙两幢楼之间的距离BD=30m,自甲楼顶端A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为26.6°,求甲、乙楼两幢楼的高度.
如图,甲乙两幢楼之间的距离BD=30m,自甲楼顶端A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为26.6°,求甲、乙楼两幢楼的高度. 已知△ABC在网格中的位置如图,那么△ABC对应的圆心坐标是
已知△ABC在网格中的位置如图,那么△ABC对应的圆心坐标是 如图,过原点O的直线与反比例函数y=
如图,过原点O的直线与反比例函数y=