题目内容
16．
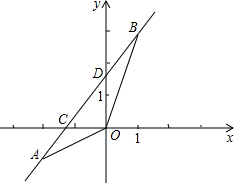如图，已知一次函数y=kx+b的图象经过A（-2a，-1），B（2-a，3）两点，并且交y轴于点D（0，1.5），且△AOB的面积为$\frac{75}{32}$，则a的值为$\frac{9}{8}$．
分析 根据三角形面积公式和△AOB的面积=S△AOD+S△BOD得出关于a的方程，解方程即可求得．
解答 解：∵△AOB的面积=S△AOD+S△BOD，
∴$\frac{1}{2}$×1.5×2a+$\frac{1}{2}$×1.5×（2-a）=$\frac{75}{32}$
解得a=$\frac{9}{8}$．
故答案为$\frac{9}{8}$．
点评 本题考查了一次函数图象上点的坐标特征，根据△AOB的面积=S△AOD+S△BOD得出关于a方程是解题的关键．
练习册系列答案
高中必刷题系列答案
相关题目
6．
如图，反比例函数y=$\frac{3}{x}$的图象与一次函数y=kx+b的图象交于A（m，3），B（-3，n）两点．
（1）求△AOB的面积；
（2）求一次函数的值小于反比例函数的值的x的取值范围．
如图，反比例函数y=$\frac{3}{x}$的图象与一次函数y=kx+b的图象交于A（m，3），B（-3，n）两点．（1）求△AOB的面积；
（2）求一次函数的值小于反比例函数的值的x的取值范围．
在如图的直角坐标系中，已知点A（1，0）；B（0，-2），将线段AB绕点A按逆时针方向旋转90°至AC．
用等分圆周的方法画下列图形．
11．已知⊙O的半径为3cm，点P是直线l上一点，OP的长为4cm，则直线l与⊙O的位置关系是（ ）
| A． | 相交 | B． | 相切 | ||
| C． | 相离 | D． | 以上三种都有可能 |
8．方程组$\left\{\begin{array}{l}{2x-y=5}\\{x-2y=1}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
5．下列说法正确的是（ ）
| A． | $\frac{t}{2}$不是整式 | B． | -2x2y与y2x是同类项 | ||
| C． | $\frac{1}{y}$是单项式 | D． | -3x2y的次数是4 |
如图，在半径为5的⊙O中，弦AB=8，P是弦AB所对的优弧上的动点，连接AP，过点A作AP的垂线交射线PA于点C，当△PAB是等腰三角形时，线段BC的长为8，$\frac{56}{15}$，$\frac{8\sqrt{5}}{3}$．