题目内容
1.已知线段AB=20cm,直线AB上有一点C,且BC=6cm,点M是线段AB的中点,点N是线段BC的中点,则MN=7或13cm.分析 根据中点的定义,可分别求出AM、BN的长度,点C存在两种情况,一种在线段AB上,一种在线段AB外,分类讨论,即可得出结论.
解答 解:依题意可知,C点存在两种情况,一种在线段AB上,一种在线段AB外.
①C点在线段AB上,如图1:
∵点M是线段AB的中点,点N是线段BC的中点,
∴AM=$\frac{AB}{2}$=10cm,BN=$\frac{BC}{2}$=3cm,
MN=AB-AM-BN=20-10-3=7cm.
②C点在线段AB外,如图2:
∵点M是线段AB的中点,点N是线段BC的中点,
∴AM=$\frac{AB}{2}$=10cm,BN=$\frac{BC}{2}$=3cm,
MN=AB-AM+BN=20-10+3=13cm.
综上得MN得长为7cm或者13cm.
故答案为:7或13.
点评 本题考查的是两点间的距离,解题的关键是注意到C点存在两种情况一种在线段AB上,一种在线段AB外.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,身高为1.6m的小明想测量一下操场边大树的高度,他沿着树影BA由B到A走去,当走到C点时,他的影子顶端正好与树的影子顶端重合,测得BC=1.4m,CA=0.7m,于是得出树的高度为( )
如图,身高为1.6m的小明想测量一下操场边大树的高度,他沿着树影BA由B到A走去,当走到C点时,他的影子顶端正好与树的影子顶端重合,测得BC=1.4m,CA=0.7m,于是得出树的高度为( )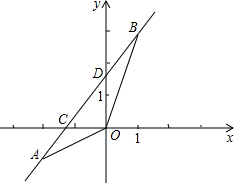 如图,已知一次函数y=kx+b的图象经过A(-2a,-1),B(2-a,3)两点,并且交y轴于点D(0,1.5),且△AOB的面积为$\frac{75}{32}$,则a的值为$\frac{9}{8}$.
如图,已知一次函数y=kx+b的图象经过A(-2a,-1),B(2-a,3)两点,并且交y轴于点D(0,1.5),且△AOB的面积为$\frac{75}{32}$,则a的值为$\frac{9}{8}$. 如图,三个边长均为2的正方形重叠在一起,O1、O2是其中两个方形的中心,求阴影部分的面积.
如图,三个边长均为2的正方形重叠在一起,O1、O2是其中两个方形的中心,求阴影部分的面积.