题目内容
已知x3+px+2有一个因式为x+1,则p的值为 .
考点:因式分解的意义
专题:
分析:此题需先将x3+px+2解成x+1,再利用分组分解法进行因式分解,即可求出另一个因式;
解答:解:设另一个因式为x2+kx+2,
则(x2+kx+2)(x+1)=x3+px+2,
x3+x2+kx2+kx+2x+2=x3+px+2,
x3+(1+k)x2+(k+2)x+2=x3+px+2,
1+k=0,k+2=p,
k=-1,p=1,
故答案为:1.
则(x2+kx+2)(x+1)=x3+px+2,
x3+x2+kx2+kx+2x+2=x3+px+2,
x3+(1+k)x2+(k+2)x+2=x3+px+2,
1+k=0,k+2=p,
k=-1,p=1,
故答案为:1.
点评:本题考查了因式分解的意义,解题时要根据分组分解法、提公因式法、公式法分解因式,难点是采用两两分组还是三一分组,要考虑分组后还能进行下一步分解,注意分解因式要彻底,直到不能再分解为止.

练习册系列答案
相关题目
有一道题“先化简,再求值:(
+
)÷
.其中a=-
”马小虎同学做题时把“a=-
”错抄成了“a=
”,但他的计算结果却与别的同学一致,也是正确的,请你解释这是怎么回事?
| a-2 |
| a+2 |
| 4a |
| a2-4 |
| 1 |
| a2-4 |
| 5 |
| 5 |
| 5 |
已知a≠0,n是正整数,那么下列各式中错误的是( )
A、a-n=
| ||
B、a-n=(
| ||
| C、a-n=-an | ||
| D、a-n=(an)-1 |
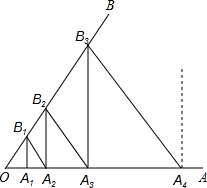 如图,已知∠AOB=60°,在OA上取OA1=1,过点A1作A1B1⊥OA交OB于点B1,过点B1作B1A2⊥OB交OA于点A2,过点A2作A2B2⊥OA交OB于点B2,过点B2作B2A3⊥OB交OA于点A3,…,按此作法继续下去,则OA10的值是
如图,已知∠AOB=60°,在OA上取OA1=1,过点A1作A1B1⊥OA交OB于点B1,过点B1作B1A2⊥OB交OA于点A2,过点A2作A2B2⊥OA交OB于点B2,过点B2作B2A3⊥OB交OA于点A3,…,按此作法继续下去,则OA10的值是 如图,在平面直角坐标系中,点A、B的坐标分别为(3,1)、(1,0),若将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标为
如图,在平面直角坐标系中,点A、B的坐标分别为(3,1)、(1,0),若将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标为 如图,在边长为6的正方形ABCD中,动点M从点A出发,沿A→B→C向终点C运动,连接DM交AC于点N,若点M运动所经过的路程为x(6≤x≤12),那么当△ADN为等腰三角形时,x的值为
如图,在边长为6的正方形ABCD中,动点M从点A出发,沿A→B→C向终点C运动,连接DM交AC于点N,若点M运动所经过的路程为x(6≤x≤12),那么当△ADN为等腰三角形时,x的值为