题目内容
4.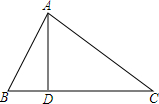 如图是一张锐角三角形纸片,AD是BC边上的高,BC=40cm,AD=20cm,现从硬纸片图上剪下一个长是宽3倍的矩形,则所剪得的矩形周长为64cm.
如图是一张锐角三角形纸片,AD是BC边上的高,BC=40cm,AD=20cm,现从硬纸片图上剪下一个长是宽3倍的矩形,则所剪得的矩形周长为64cm.
分析 根据矩形性质得出∠AHG=∠ABC,再证明△AHG∽△ABC,利用相似三角形对应边的比等于相似比列出比例式即可求出HE的长度,以及矩形的周长.
解答 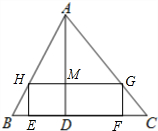 解:∵四边形EFGH为矩形,
解:∵四边形EFGH为矩形,
∴EF∥GH,
∴∠AHG=∠ABC,
又∵∠HAG=∠BAC,
∴△AHG∽△ABC,
∴$\frac{AM}{AD}$=$\frac{HG}{BC}$;
设HE=xcm,MD=HE=xcm,
∵AD=20cm,
∴AM=20-x,
∵HG=2HE,
∴HG=3x,
可得 $\frac{20-x}{20}$=$\frac{3x}{40}$,
解得x=8,
3x=24,
所以矩形EFGH的周长为:2×(8+24)=64(cm).
故答案为:64.
点评 此题主要考查了相似三角形的判定与性质,根据矩形性质得出△AHG∽△ABC是解决问题的关键.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
12.x2+px+q=0(p≠0)的两个根为相等的实数,则x2-qx+p2=0的两个根为( )
| A. | 非实数 | B. | 相等两实数 | ||
| C. | 非实数或相等两实数 | D. | 实数 |
9.新华网成都9月26日电(记者 常烨 徐倩)第十二届华商大会四川世界华商合作交流会暨项目签约仪式26日在中国成都举行,大会活动期间共签约合作项目241个,总投资额为1323亿元,请用科学记数法表示总投资额正确的是( )
| A. | 132.3×108元 | B. | 13.23×1010元 | C. | 1.323×1012元 | D. | 1.323×1011元 |