题目内容
14.先化简,再求值:($\frac{3x}{x-2}-\frac{x}{x+2}$)$÷\frac{x}{{x}^{2}-4}$,其中x=(-$\frac{1}{2}$)-1+π0.分析 首先把除法转化为乘法,然后利用分配律转化为乘法,然后合并同类项即可化简,然后把x的值进行化简,然后代入求解即可.
解答 解:原式=$\frac{3x}{x-2}$•$\frac{(x+2)(x-2)}{x}$-$\frac{x}{x+2}$•$\frac{(x+2)(x-2)}{x}$
=3(x+2)-(x-2)
=3x+6-x+2
=2x+8,
当x=(-$\frac{1}{2}$)-1+π0=-2+1=-1时,原式=-2+8=6.
点评 本题综合考查了分式的化简求值,分式混合运算要注意先去括号;分子、分母能因式分解的先因式分解;除法要统一为乘法运算.

练习册系列答案
相关题目
4. 如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=( )
如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=( )
 如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=( )
如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=( )| A. | 195° | B. | 250° | C. | 270° | D. | 无法确定 |
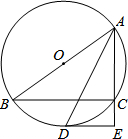 如图,AB是⊙O的直径,C为⊙O上一点,AD平分∠BAC交⊙O于点D,DE∥BC交AC延长线于点E.
如图,AB是⊙O的直径,C为⊙O上一点,AD平分∠BAC交⊙O于点D,DE∥BC交AC延长线于点E.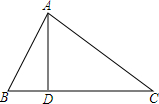 如图是一张锐角三角形纸片,AD是BC边上的高,BC=40cm,AD=20cm,现从硬纸片图上剪下一个长是宽3倍的矩形,则所剪得的矩形周长为64cm.
如图是一张锐角三角形纸片,AD是BC边上的高,BC=40cm,AD=20cm,现从硬纸片图上剪下一个长是宽3倍的矩形,则所剪得的矩形周长为64cm.