题目内容
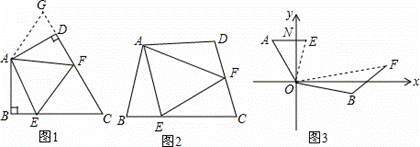
如图，在等腰直角三角形ABC和DEC中，∠BCA=∠DCE=90°，点E在边AB上，ED与AC交于点F，连接AD．
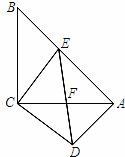
（1）求证：△BCE≌△ACD．
（2）求证：AB⊥AD．
【解析】（1）由题意知∠BCE+∠ECA=∠ECA+∠ACD=90°，∴∠BCE=∠ACD，
又∵BC=AC，CE=CD，∴△BCE≌△ACD．
（2）由（1）知，∠B=∠CAD，又∵∠B+∠CAE=90°，∴∠CAD+∠CAE=90°，即∠DAE=90°，
∴AB
⊥AD．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，则此扇形的弧长为 ．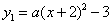
与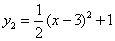
交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．则以下结论：①无论x取何值，
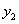的值总是正数；②
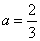；③当x=0时，
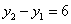；④AB+AC=10；⑤
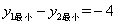，其中正确结论的个数是： ．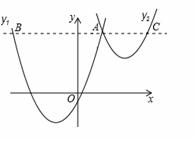
∠BAD，上述结论是否仍然成立，并说明理由；
米，那么下列方程正确的是（ ）
B．
D．
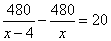
）2+（tan45°）–1