��Ŀ����
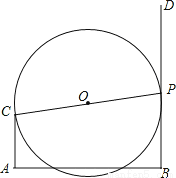
��ͼ��CA��AB��DB��AB����֪AC=2��AB=6����P����BD��һ���㣬��CPΪֱ������O����P�˶�ʱ������O���߶�AB�й����㣬��BP���ֵΪ ��
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ��CA��AB��DB��AB����֪AC=2��AB=6����P����BD��һ���㣬��CPΪֱ������O����P�˶�ʱ������O���߶�AB�й����㣬��BP���ֵΪ ��
