题目内容
15.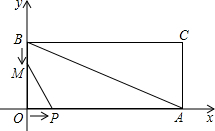 如图,在平面直角坐标系xOy中,已知矩形OACB的边OA,OB分别在x轴上和y轴上,线段OA,OB的长分别是一元二次方程x2-18x+72=0的两个根,且OA>OB;点P从点O开始沿OA边匀速移动,点M从点B开始沿BO边匀速移动.如果点P,点M同时出发,它们移动的速度相同,设OP=x(0≤x≤6),设△POM的面积为y.
如图,在平面直角坐标系xOy中,已知矩形OACB的边OA,OB分别在x轴上和y轴上,线段OA,OB的长分别是一元二次方程x2-18x+72=0的两个根,且OA>OB;点P从点O开始沿OA边匀速移动,点M从点B开始沿BO边匀速移动.如果点P,点M同时出发,它们移动的速度相同,设OP=x(0≤x≤6),设△POM的面积为y.(1)求y与x的函数关系式;
(2)连接矩形的对角线AB,当x为何值时,以P,O,M为顶点的三角形与△AOB相似.
分析 (1)首先根据线段OA,OB的长分别是一元二次方程x2-18x+72=0的两个根,且OA>OB,求出OA、OB的长度各是多少;然后根据直角三角形面积的求法,求出y与x的函数关系式即可.
(2)根据题意,分两种情况:①当△MOP∽△AOB时;②当△POM∽△AOB时;然后根据三角形相似的性质,求出x为何值时,以P,O,M为顶点的三角形与△AOB相似即可.
解答 解:(1)如图1,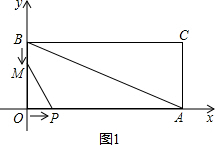 ,
,
由x2-18x+72=0,解得
x1=12,x2=6,
∵线段OA,OB的长分别是一元二次方程x2-18x+72=0的两个根,且OA>OB,
∴OA=12,OB=6,
∵OP=BM=x,
∴OM=6-x,
∴S△POM=$\frac{1}{2}OM•OP$=$\frac{1}{2}$(6-x)x=-$\frac{1}{2}$x2+3x,
即y=-$\frac{1}{2}$x2+3x(0≤x≤6).
(2)①如图2,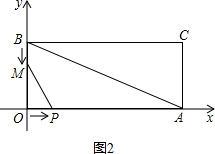 ,
,
当△MOP∽△AOB时,
可得$\frac{MO}{AO}=\frac{OP}{OB}$,
∴$\frac{6-x}{12}=\frac{x}{6}$,
解得x=2.
②如图3,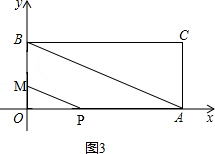 ,
,
当△POM∽△AOB时,
可得$\frac{PO}{AO}=\frac{OM}{OB}$,
∴$\frac{x}{12}=\frac{6-x}{6}$,
解得x=4.
综上,可得
当x=2或x=4时,以P,O,M为顶点的三角形与△AOB相似.
点评 (1)此题主要考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.
(2)此题还考查了函数解析式的求法,以及三角形的面积的求法,要熟练掌握.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | ±2014 | B. | -2014 | C. | 2014 | D. | 2018 |
| 实际身高/cm | 110 | 97 | 118 | 108 | 111 | 100 | 101 | 96 | 113 | 116 |
| 相对身高/cm |
(2)根据相对身高=实际身高-基准数,结合你选取的基准数,用正、负数填写表格;
(3)这10名学生的平均身高是多少?
| A. | 27 | B. | 28 | C. | 29 | D. | 30 |
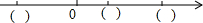 有理数a<0、b>0、c>0,且|b|<|a|<|c|,
有理数a<0、b>0、c>0,且|b|<|a|<|c|,
 如图,在△ABC中,∠C=∠ABC=2∠A,BD⊥AC于D,求∠DBC的度数.
如图,在△ABC中,∠C=∠ABC=2∠A,BD⊥AC于D,求∠DBC的度数.