题目内容
19. 如图,在△ABC中,已知DE∥BC,AD=5,DB=10,DE=3.
如图,在△ABC中,已知DE∥BC,AD=5,DB=10,DE=3.(1)求$\frac{AE}{EC}$的值;
(2)求BC的长.
分析 (1)根据平行线分线段成比例定理得到答案;
(2)根据平行线分线段成比例定理得到答案.
解答 解:(1)∵DE∥BC,
∴$\frac{AE}{EC}=\frac{AD}{DB}$=$\frac{5}{10}$=$\frac{1}{2}$;
(2)∵DE∥BC,
∴$\frac{DE}{BC}$=$\frac{AD}{AB}$=$\frac{5}{5+10}$=$\frac{1}{3}$,
即$\frac{3}{BC}=\frac{1}{3}$,
解得:BC=9.
点评 本题考查了平行线分线段成比例定理,掌握定理的应用是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10. 如图,AB、CD为⊙O的两条弦,已知AB⊥CD于点E,OF⊥AB于点F,已知AC=4$\sqrt{5}$,
如图,AB、CD为⊙O的两条弦,已知AB⊥CD于点E,OF⊥AB于点F,已知AC=4$\sqrt{5}$,
BD=6$\sqrt{5}$,EF=1,则OE的长是( )
 如图,AB、CD为⊙O的两条弦,已知AB⊥CD于点E,OF⊥AB于点F,已知AC=4$\sqrt{5}$,
如图,AB、CD为⊙O的两条弦,已知AB⊥CD于点E,OF⊥AB于点F,已知AC=4$\sqrt{5}$,BD=6$\sqrt{5}$,EF=1,则OE的长是( )
| A. | 3 | B. | 4 | C. | $\sqrt{17}$ | D. | 4$\sqrt{5}$ |
4.下列事件是随机事件的是( )
| A. | 画一个三角形其内角和为361° | |
| B. | 任意做一个矩形,其对角线相等 | |
| C. | 任取一个实数,其相反数之和为0 | |
| D. | 外观相同的10件同种产品中有2件是不合格产品,现从中抽取一件恰为合格品 |
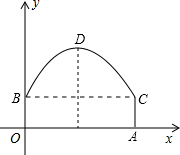 如图,隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,建立直角坐标系,抛物线可用y=-$\frac{1}{6}$x2+bx+c表示.
如图,隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,建立直角坐标系,抛物线可用y=-$\frac{1}{6}$x2+bx+c表示. 如图,已知在平面直角坐标系xOy中,二次函数y=-x2+mx+n的图象经过点A(3,0),B(m,m+1),且与y轴相交于点C.
如图,已知在平面直角坐标系xOy中,二次函数y=-x2+mx+n的图象经过点A(3,0),B(m,m+1),且与y轴相交于点C.