题目内容
 已知如图,△ABC中,AD为BC的中线,E为AD的中点,延长CE交AB于点F,求
已知如图,△ABC中,AD为BC的中线,E为AD的中点,延长CE交AB于点F,求| AF |
| BF |
考点:三角形中位线定理,平行线分线段成比例
专题:
分析:可过点D作DG∥CF,交AB于点G,则可知DG为△BCF的中位线,EF为△ADG的中位线,可知G、F为AB的三等分点,可求得
;或过D作DM∥AB,交CF于点M,则DM为△BCF的中位线,且可证得△DEM≌△AEF,可得到DM=AF=
BF,可求得比值.
| AF |
| BF |
| 1 |
| 2 |
解答:解:方法一:
过点D作DG∥CF,交AB于点G,如图1,

∵D为BC中点,
∴G为BF中点,
∴BG=GF,
同理可得F为AG中点,则有AF=GF,
∴BF=2AF,
∴
=
;
方法二:
过D作DM∥AB,交CF于点M,如图2,

∵D为BC中点,
∴M为CF中点,
∴DM=
BF,
∵E为AD中点,
∴AE=DE,且∠EFA=∠EMD,
在△AEF和△DEM中,
,
∴△AEF≌△DEM(AAS),
∴DM=AF,
∴
=
.
过点D作DG∥CF,交AB于点G,如图1,

∵D为BC中点,
∴G为BF中点,
∴BG=GF,
同理可得F为AG中点,则有AF=GF,
∴BF=2AF,
∴
| AF |
| BF |
| 1 |
| 2 |
方法二:
过D作DM∥AB,交CF于点M,如图2,

∵D为BC中点,
∴M为CF中点,
∴DM=
| 1 |
| 2 |
∵E为AD中点,
∴AE=DE,且∠EFA=∠EMD,
在△AEF和△DEM中,
|
∴△AEF≌△DEM(AAS),
∴DM=AF,
∴
| AF |
| BF |
| 1 |
| 2 |
点评:本题主要考查三角形中位线定理的逆定理,充分利用题目中的两个中点,作出平行线是解题的关键.

练习册系列答案
相关题目
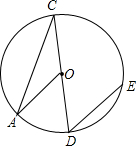 如图,CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠A的度数为( )
如图,CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠A的度数为( )| A、50° | B、40° |
| C、30° | D、25° |
若方程3x+5=17的解也是关于x的方程
-a=4的解,则a的值为( )
| x |
| 2 |
| A、-6 | B、2 | C、16 | D、-2 |
若|a|=-a,则实数a在数轴上的对应点一定在( )
| A、原点左侧 |
| B、原点或原点左侧 |
| C、原点右侧 |
| D、原点或原点右侧 |
 如图,在△ACB中,∠C=90°,∠CAB与∠CBA的角平分线交于点D,AC=3,
如图,在△ACB中,∠C=90°,∠CAB与∠CBA的角平分线交于点D,AC=3,
 如图,∠A=30°,∠B′=62°,△ABC与△A′B′C′关于直线l对称,则△ABC中的∠C=
如图,∠A=30°,∠B′=62°,△ABC与△A′B′C′关于直线l对称,则△ABC中的∠C= 如图,已知过A、C、D三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=57°,那么∠ABC=
如图,已知过A、C、D三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=57°,那么∠ABC=