题目内容
3.已知:如图,AB∥CD,线段EF分别与AB,CD相交于点E,F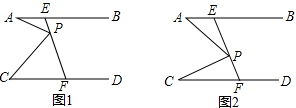
(1)如图1,已知∠A=30°,∠APC=80°,求∠C的度数;
(2)如图2,当动点P在线段EF上运动时(不包括E,F两点),∠A,∠APC与∠C之间有何数量关系?并证明你的结论;
(3)当动点P在直线EF(线段EF除外)上运动时,(2)中的结论是否仍然成立?如果不成立,请直接写出∠A,∠APC与∠C之间的数量关系.
分析 (1)过P作PO∥AB,推出AB∥PO∥CD,根据平行线性质得出∠APO=∠A=30°,∠C=∠CPO,代入求出即可;
(2)过P作PO∥AB,推出AB∥PO∥CD,根据平行线性质得出∠APO=∠A,∠C=∠CPO,求出即可;
(3)过P作PO∥AB,推出AB∥PO∥CD,根据平行线性质得出∠APO=∠A,∠C=∠CPO,求出即可.
解答  解:(1)如图①,过P作PO∥AB,
解:(1)如图①,过P作PO∥AB,
∵AB∥CD,
∴AB∥PO∥CD,
∵∠A=30°,
∴∠APO=∠A=30°,∠C=∠CPO,
∵∠APC=80°
∴∠C=∠CPO=∠APC-∠APO=80°-30°=50°;
(2)∠A+∠C=∠APC,
证明:如图②,过P作PO∥AB,
∵AB∥CD,
∴AB∥PO∥CD,
∴∠APO=∠A,∠C=∠CPO,
∴∠APC=∠APO+∠CPO=∠A+∠C;
(3)不成立,关系式是:∠A-∠C=∠APC,
理由:如图③,过P作PO∥AB,
∵AB∥CD,
∴AB∥PO∥CD,
∴∠APO=∠A,∠C=∠CPO,
∴∠A-∠C=∠APO-∠CPO=∠APC,
即∠A-∠C=∠APC.
点评 本题考查了平行线性质的应用,在解答此题时要注意作出辅助线,构造出平行线求解.

练习册系列答案
相关题目
14.方程x2-3x=0的根是( )
| A. | x=3 | B. | x1=3,x2=-3 | C. | x1=$\sqrt{3}$,x2=-$\sqrt{3}$ | D. | x1=0,x2=3 |
12.下列说法中正确的是( )
| A. | 已知a,b,c是三角形的三边,则a2+b2=c2 | |
| B. | 在直角三角形中两边和的平方等于第三边的平方 | |
| C. | 在Rt△ABC中,∠C=90°,所以BC2+AC2=AB2 | |
| D. | 在Rt△ABC中,∠B=90°,所以BC2+AC2=AB2 |
 画出几何体的主视图、左视图和俯视图.
画出几何体的主视图、左视图和俯视图. 如图,四边形ABCD是菱形,BC=5cm,BD=6cm,DH⊥AB于点H,则DH=4.8cm.
如图,四边形ABCD是菱形,BC=5cm,BD=6cm,DH⊥AB于点H,则DH=4.8cm.