题目内容
19．
如图，△ABC中，∠B=26°，∠C=70°，AD平分∠BAC，AE⊥BC于E，EF⊥AD于F，求∠DEF的度数．
分析 先根据三角形内角和定理求出∠BAC度数，再根据角平分线的性质求出∠BAD的度数，再根据三角形外角的性质求出∠ADE的度数，由EF⊥AD可知∠DFE=90°，再由两角互余的性质是解答此题的关键．
解答 解：∵△ABC中，∠B=26°，∠C=70°，
∴∠BAC=180°-26°-70°=84°．
∵AD平分∠BAC，
∴BAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×84°=42°．
∵∠ADE是△ABD的外角，
∴∠ADE=∠B+∠BAD=26°+42°=68°．
∵EF⊥AD于F，
∴∠DFE=90°，
∴∠DEF=90°-68°=22°．
点评 本题考查的是三角形内角形内角和定理，熟知三角形内角和是180°是解答此题的关键．
练习册系列答案
相关题目
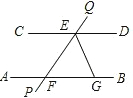如图，AB∥CD，直线PQ分别交AB、CD于点E、F，EG是∠FED的平分线，交AB于点G．若∠QED=40°，那么∠EGB等于110°．
8．下列式子中，正确的是（ ）
| A． | $\sqrt{25}$=±5 | B． | ±$\sqrt{25}$=5 | C． | $\sqrt{{（{-5}）}^2}$=5 | D． | $\sqrt{{（{-3}）}^2}$=-3 |