题目内容
2.(1)已知:如图1,点O为直线AB上任意一点,射线OC为任意一条射线.OD、OE分别平分∠AOC和∠BOC,则∠DOE=90°;(2)已知:如图2,点O为直线AB上任意一点,射线OC为任意一条射线,其中∠COD=$\frac{1}{3}$∠AOC,∠COE=$\frac{1}{3}$∠BOC,求∠DOE得度数;
(3)如图3,点O为直线AB上任意一点,OD是∠AOC的平分线,OE在∠BOC内,∠COE=$\frac{1}{3}$∠BOC,∠DOE=72°,求∠BOE的度数.

分析 (1)根据角平分线的定义得到∠DOE=$\frac{1}{2}$∠AOB=90°;
(2)根据∠COD=$\frac{1}{3}$∠AOC,∠COE=$\frac{1}{3}$∠BOC和平角的定义即可得到结论;
(3)设∠BOC=x°则∠COE=$\frac{1}{3}$x°,∠BOE=$\frac{2}{3}$x°,∠AOC=(180-x)°,由OD是∠AOC的平分线,得到∠COD=$\frac{1}{2}$∠AOC=(90-$\frac{1}{2}$x)°,根据已知条件列方程即可得到结论.
解答 解:(1)∵OD、OE分别平分∠AOC和∠BOC,
∴∠COD=$\frac{1}{2}∠$AOC,∠COE=$\frac{1}{2}∠$BOC,
∵∠AOB=180°,
∴∠DOE=∠COD+∠COE=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}∠AOB=90°$;
故答案为:90°;
(2)∵∠COD=$\frac{1}{3}$∠AOC,∠COE=$\frac{1}{3}$∠BOC,
∴∠DOE=∠COD+∠COE,
=$\frac{1}{3}$∠AOC+$\frac{1}{3}$∠BOC=$\frac{1}{3}$(∠AOC+∠BOC)=$\frac{1}{3}$∠AOB=60°;
(3)设∠BOC=x°则∠COE=$\frac{1}{3}$x°,∠BOE=$\frac{2}{3}$x°,∠AOC=180°-x°,
∵OD是∠AOC的平分线,
∴∠COD=$\frac{1}{2}$∠AOC=90°-$\frac{1}{2}$x°,
∵∠DOE=72°,
∴90°-$\frac{1}{2}$x°+$\frac{1}{3}$x°=72°,
解得:x=108,
∴∠BOE=$\frac{2}{3}$×108°=72°.
点评 本题考查了角平分线的定义.根据角平分线定义得出所求角与已知角的关系转化求解.

 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2016次碰到矩形的边时,点P的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2016次碰到矩形的边时,点P的坐标为( )| A. | (0,3) | B. | (5,0) | C. | (1,4) | D. | (8,3) |
 (1)在6×6的网格中(每个小正方形边长均为1).画出一个面积为10的正方形;
(1)在6×6的网格中(每个小正方形边长均为1).画出一个面积为10的正方形; 如图,△ABC中,E、F分别是AB、AC上的两点,且$\frac{AE}{EB}=\frac{AF}{FC}=\frac{1}{2}$,若△AEF的面积为3,则四边形EBCF的面积为24.
如图,△ABC中,E、F分别是AB、AC上的两点,且$\frac{AE}{EB}=\frac{AF}{FC}=\frac{1}{2}$,若△AEF的面积为3,则四边形EBCF的面积为24.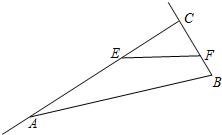 如图,在Rt△ABC中,∠ACB=90°,AC=12cm,BC=4cm,点E从点C出发沿射线CA以每秒3cm的速度运动,同时点F从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=12cm,BC=4cm,点E从点C出发沿射线CA以每秒3cm的速度运动,同时点F从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.