题目内容
13. (1)在6×6的网格中(每个小正方形边长均为1).画出一个面积为10的正方形;
(1)在6×6的网格中(每个小正方形边长均为1).画出一个面积为10的正方形;(2)在数轴上找到表示-$\sqrt{5}$的点.
分析 (1)由正方形的性质和勾股定理即可得出结果;
(2)根据勾股定理可以知道,一个直角三角形的斜边为2,一直角边为1时,另一直角边为$\sqrt{5}$,在数轴上画出即可,-$\sqrt{5}$在原点的左边.
解答 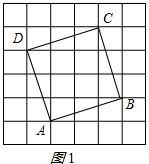 解:(1)∵面积为10的正方形的边长为$\sqrt{10}$,
解:(1)∵面积为10的正方形的边长为$\sqrt{10}$,
$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴四边形ABCD即为所求,
如图1所示:
(2)如图2所示:
以原点O为圆心,所画直角边的斜边OB为半径画弧,
交数轴的负半轴于一点C,
点C即为表示-$\sqrt{5}$的点.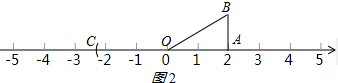
点评 本题考查了勾股定理的应用、正方形的性质、实数与数轴;注意:在直角三角形中,两直角边的平方和等于斜边的平方.

练习册系列答案
相关题目
1.将二次函数y=x2的图象向下平移1个单位,则平移后的二次函数的解析式为( )
| A. | y=x2-1 | B. | y=x2+1 | C. | y=(x-1)2 | D. | y=(x+1)2 |
8.玉树地震后,青海省某乡镇中学的同学用下面的方法检测教室的房梁是否水平:如图,在等腰直角三角尺斜边中点栓一条细绳,细绳的另一端挂一个铅锤,把这块三角尺的斜边贴在房梁上,结果绳子经过三角尺的直角顶点,于是同学们确信房梁是水平的,其理由是( )
| A. | 等腰三角形两腰等分 | |
| B. | 等腰三角形两底角相等 | |
| C. | 三角形具有稳定性 | |
| D. | 等腰三角形的底边中线和底边上的高重合 |
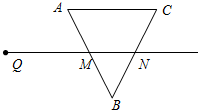 如图,射线QN与边长为8的等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN.动点P从点Q出发,沿射线QN以每秒2cm的速度向右移动,以点P为圆心,2$\sqrt{3}$cm为半径的圆也随之移动.若AM=MB=4cm,QM=8cm,且经过t秒,当⊙P与△ABC的边相切时,则t可取的一切值为t=2或3≤t≤7或t=8(单位:秒).
如图,射线QN与边长为8的等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN.动点P从点Q出发,沿射线QN以每秒2cm的速度向右移动,以点P为圆心,2$\sqrt{3}$cm为半径的圆也随之移动.若AM=MB=4cm,QM=8cm,且经过t秒,当⊙P与△ABC的边相切时,则t可取的一切值为t=2或3≤t≤7或t=8(单位:秒).

 如图所示,已知长方形的长为a米,宽为b米,半圆半径为r米.
如图所示,已知长方形的长为a米,宽为b米,半圆半径为r米.