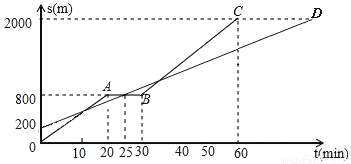
��Ŀ����
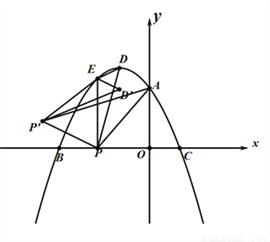
��ͼ����ƽ��ֱ������ϵ�У�������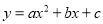 ��x�ύ��B����3��0����C��1��0�����㣬��y�ύ�ڵ�A��0��2���������ߵĶ���ΪD������AB����E�ǵڶ������ڵ��������ϵ�һ���㣬����E��EP��BC�ڵ�P�����߶�AB�ڵ�F��
��x�ύ��B����3��0����C��1��0�����㣬��y�ύ�ڵ�A��0��2���������ߵĶ���ΪD������AB����E�ǵڶ������ڵ��������ϵ�һ���㣬����E��EP��BC�ڵ�P�����߶�AB�ڵ�F��
��1����������ߵĽ���ʽ��
��2������E��EG��AB�ڵ�G��QΪ�߶�AC���е㣬����EGF�ܳ����ʱ���� ������һ��R��ʹ��|RE��RQ|ֵ��������R������꼰|RE��RQ|�����ֵ��
������һ��R��ʹ��|RE��RQ|ֵ��������R������꼰|RE��RQ|�����ֵ��
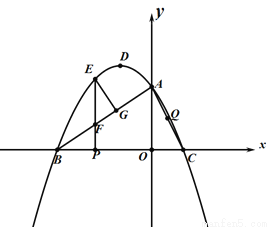
��3���ڣ�2���������£�����PED��E����ת�á�ED��P�䣬����AP��P����APΪֱ�DZߵ�ֱ��������ʱ�����P������꣮
��ϰ��ϵ�д�
 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�
�����Ŀ
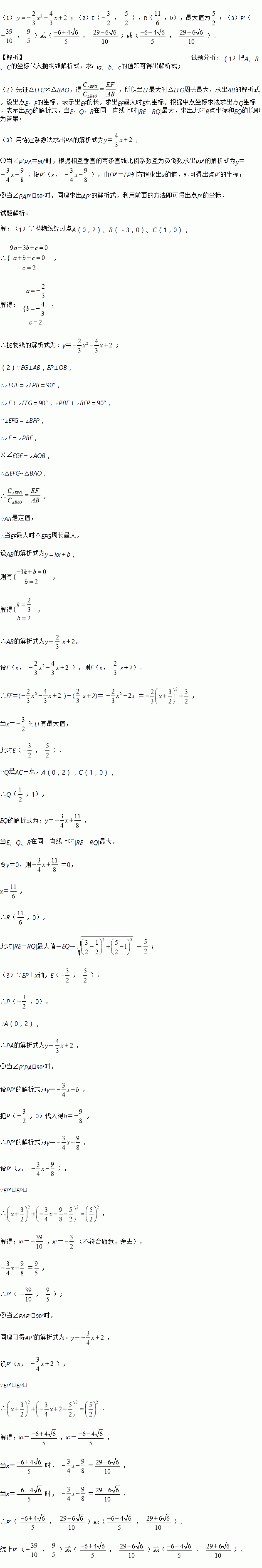

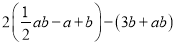 ������
������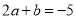 .
.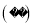
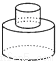
 B.
B. 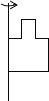 C.
C. 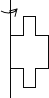 D.
D. 
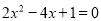 �� ��2��
�� ��2��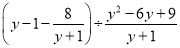 ��
��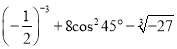 ��____________��
��____________��