题目内容
7.(1)(-12)-(-20)+(-8)-15.(2)-$\frac{1}{4}×(+3)÷(-\frac{1}{2})^{3}$.
(3)19$\frac{1}{2}$×$\frac{1}{9}$+(-1.5)÷(-3)2.
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式先计算乘方运算,再计算乘除运算即可得到结果;
(3)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
解答 解:(1)原式=-12+20-8-15=-35+20=-15;
(2)原式=-$\frac{1}{4}$×3×(-8)=6;
(3)原式=19.5×$\frac{1}{9}$-1.5×$\frac{1}{9}$=(19.5-1.5)×$\frac{1}{9}$=18×$\frac{1}{9}$=2.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
17.计算8×(-$\frac{1}{2}$)的结果是( )
| A. | 16 | B. | -16 | C. | -4 | D. | 4 |
18.若不等式0≤x+1<3的解中至少有一个能使关于x的一次不等式2x>a+3成立,则a的取值范围是( )
| A. | a≤1 | B. | a≥1 | C. | a≥-5 | D. | a<1 |
2.下列说法中,正确的是( )
①射线AB和射线BA是同一条射线;
②若AB=BC,则点B为线段AC的中点;
③同角的补角相等;
④点C在线段AB上,M,N分别是线段AC,CB的中点.若MN=5,则线段AB=10.
①射线AB和射线BA是同一条射线;
②若AB=BC,则点B为线段AC的中点;
③同角的补角相等;
④点C在线段AB上,M,N分别是线段AC,CB的中点.若MN=5,则线段AB=10.
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
19.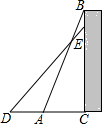 如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )
如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )
 如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )
如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )| A. | 0.4 | B. | 0.6 | C. | 0.7 | D. | 0.8 |
16. 某校要举办国庆联欢会,主持人站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20m,C为AB的一个黄金分割点(AC<BC),则AC的长为(结果精确到0.1m)( )
某校要举办国庆联欢会,主持人站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20m,C为AB的一个黄金分割点(AC<BC),则AC的长为(结果精确到0.1m)( )
 某校要举办国庆联欢会,主持人站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20m,C为AB的一个黄金分割点(AC<BC),则AC的长为(结果精确到0.1m)( )
某校要举办国庆联欢会,主持人站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20m,C为AB的一个黄金分割点(AC<BC),则AC的长为(结果精确到0.1m)( )| A. | 6.7m | B. | 7.6m | C. | 10m | D. | 12.4m |
17.已知一次函数y=(m-2)x+3的图象经过第一、二、四象限,则m的取值范围是( )
| A. | m<0 | B. | m>0 | C. | m<2 | D. | m>2 |
 从2016年1月1日开始,北京市居民生活用气阶梯价格制度将正式实施,一般生活用气收费标准如下表所示,比如6口以下的户年天然气用量在第二档时,其中350立方米按2.28元/m3收费,超过350立方米的部分按2.5元/m3收费.小冬一家有五口人,他想帮父母计算一下实行阶梯价后,家里天然气费的支出情况.
从2016年1月1日开始,北京市居民生活用气阶梯价格制度将正式实施,一般生活用气收费标准如下表所示,比如6口以下的户年天然气用量在第二档时,其中350立方米按2.28元/m3收费,超过350立方米的部分按2.5元/m3收费.小冬一家有五口人,他想帮父母计算一下实行阶梯价后,家里天然气费的支出情况.