题目内容
15.一般情况下$\frac{a}{2}+\frac{b}{3}=\frac{a+b}{2+3}$不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得$\frac{a}{2}+\frac{b}{3}=\frac{a+b}{2+3}$成立的一对数a,b为“相伴数对”,记为(a,b).(1)若(1,b)是“相伴数对”,求b的值;
(2)写出一个“相伴数对”(a,b),其中a≠0,且a≠1;
(3)若(m,n)是“相伴数对”,求代数式m-$\frac{22}{3}n$-[4m-2(3n-1)]的值.
分析 (1)利用“相伴数对”的定义化简,计算即可求出b的值;
(2)写出一个“相伴数对”即可;
(3)利用“相伴数对”定义得到9m+4n=0,原式去括号整理后代入计算即可求出值.
解答 解:(1)∵(1,b)是“相伴数对”,
∴$\frac{1}{2}$+$\frac{b}{3}$=$\frac{1+b}{2+3}$,
解得:b=-$\frac{9}{4}$;
(2)(2,-$\frac{9}{2}$)(答案不唯一);
(3)由(m,n)是“相伴数对”可得:$\frac{m}{2}$+$\frac{n}{3}$=$\frac{m+n}{2+3}$,即$\frac{3m+2n}{6}$=$\frac{m+n}{5}$,
即9m+4n=0,
则原式=m-$\frac{22}{3}$n-4m+6n-2=-$\frac{4}{3}$n-3m-2=-$\frac{9m+4n}{3}$-2=-2.
点评 此题考查了整式的加减,以及代数式求值,弄清题中的新定义是解本题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
5.-x8等于( )
| A. | (-x)2•x6 | B. | -x3•(-x)5 | C. | -x•(-x)7 | D. | -x4•(-x)4 |
6.下列图形中,是中心对称图形的为( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.空调常使用的三种制冷剂的沸点如下表所示,那么这三种制冷剂按沸点从低到高排列的顺序是( )
| 制冷剂编号 | R22 | R12 | R410A |
| 制冷剂 | 二氟一氯甲烷 | 二氟二氯甲烷 | 二氟甲烷50%,五氟乙烷50% |
| 沸点近似值 (精确到1℃) | -41 | -30 | -52 |
| A. | R12,R22,R410A | B. | R22,R12,R410A | C. | R410A,R12,R22 | D. | R410A,R22,R12 |
4.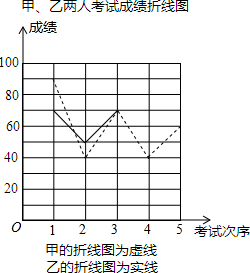 甲、乙两位同学5次数学成绩统计如表,他们的5次总成绩相同,小明根据他们的成绩绘制了尚不完整的统计图表,请同学们完成下列问题.
甲、乙两位同学5次数学成绩统计如表,他们的5次总成绩相同,小明根据他们的成绩绘制了尚不完整的统计图表,请同学们完成下列问题.
甲、乙两人的数学成绩统计表
(1)a=40,$\overline{x_乙}$=60;
(2)请完成图中表示乙成绩变化情况的折线;
(3)S甲2=360,乙成绩的方差是160,可看出乙的成绩比较稳定(填“甲”或“乙”).从平均数和方差的角度分析,乙将被选中.
 甲、乙两位同学5次数学成绩统计如表,他们的5次总成绩相同,小明根据他们的成绩绘制了尚不完整的统计图表,请同学们完成下列问题.
甲、乙两位同学5次数学成绩统计如表,他们的5次总成绩相同,小明根据他们的成绩绘制了尚不完整的统计图表,请同学们完成下列问题.| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 甲成绩 | 90 | 40 | 70 | 40 | 60 |
| 乙成绩 | 70 | 50 | 70 | a | 70 |
(1)a=40,$\overline{x_乙}$=60;
(2)请完成图中表示乙成绩变化情况的折线;
(3)S甲2=360,乙成绩的方差是160,可看出乙的成绩比较稳定(填“甲”或“乙”).从平均数和方差的角度分析,乙将被选中.
 如图所示,在三角形ABC中,点D是边AB上的一点.已知∠ACB=90°,∠CDB=90°,则图中与∠A互余的角的个数是( )
如图所示,在三角形ABC中,点D是边AB上的一点.已知∠ACB=90°,∠CDB=90°,则图中与∠A互余的角的个数是( )