Question

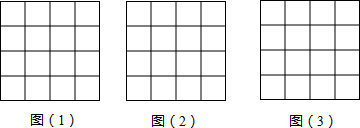
5．如图，正方形网格中每个正方形的边长都是1，每个小格的顶点叫做格点，以格点为顶点，分别按下列要求画三角形．
（1）其中一条边为无理数，两条边为有理数；
（2）其中两条边为无理数，一条边为有理数；
（3）三条边都能为无理数吗？若能在图（3）中画出，这些三角形的面积都是2（填有理数或无理数），并计算出你所画三角形的面积．

Answer 1

分析 （1）和（2）按要求画出三角形；
（2）按要求画出三角形，利用面积差求△ABC的面积．

解答 解：（1）如图1，AC=1，AB=2，BC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$；
则△ABC就是符合条件的三角形；
（2）如图2，AF=3，DE=$\sqrt{5}$，EF=2$\sqrt{2}$，则△DEF就是符合条件的三角形；

（3）如图3，AB=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$，BC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$，AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，
∴△ABC就是符合条件的三角形；
S_△ABC=S_{长方形DECF}-S_△ABD-S_△AFC-S_△BEC，
=2×3-$\frac{1}{2}$×1×1-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×2，
=2．

点评 本题是作图题，一方面考查了三角形的画法及有理数与无理数的判别，另一方面还考查了勾股定理及三角形面积的求法；本题要熟练掌握勾股定理的运用，用格点作边是有理数，用长方形对角线作边就是无理数．