题目内容
11.若$\frac{a+b}{a-b}$=$\frac{b+c}{2(b-c)}$=$\frac{a+c}{2(c-a)}$,求8a+9b+5c的值.分析 设$\frac{a+b}{a-b}$=$\frac{b+c}{2(b-c)}$=$\frac{a+c}{2(c-a)}$=k,则a+b=k(a-b),b+c=2k(b-c),(c+a)=3k(c-a),再把三式相加即可得出结论.
解答 解:∵设$\frac{a+b}{a-b}$=$\frac{b+c}{2(b-c)}$=$\frac{a+c}{2(c-a)}$=k,则a+b=k(a-b),b+c=2k(b-c),(c+a)=3k(c-a)
∴6(a+b)=6k(a-b)①,3(b+c)=6k(b-c)②,2(c+a)=6k(c-a)③.
①+②+③得,6(a+b)+3(b+c)+2(c+a)=6k(a-b+b-c+c-a),即8a+9b+5c=0
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
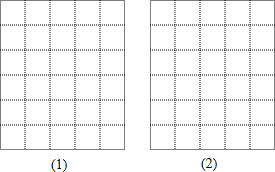 如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画三角形和平行四边形.
如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画三角形和平行四边形.