题目内容
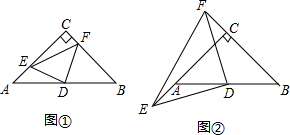
8.在Rt△ABC中,∠ACB=90°,AC=BC,D为边AB中点,点E、F分别在射线CA、BC上,且AE=CF,连结EF.猜想:如图①,当点E、F分别在边CA和BC上时,线段DE与DF的大小关系为DE=DF.
探究:如图②,当点E、F分别在边CA、BC的延长线上时,判断线段DE与DF的大小关系,并加以证明.
应用:如图②,若DE=4,利用探究得到的结论,求△DEF的面积.
分析 猜想:连接CD,可证明△ADE≌△CFD,可得出结论;
探究:连接CD,同(1)可证明△ADE≌△CFD,可证得DE=DF;
应用:由△ADE≌△CFD可证得∠EDF=90°,容易求得△DEF的面积.
解答 猜想:DE=DF.
如图1,连结CD,
∵∠ACB=90°,AC=BC,
∴∠CAD=45°,
∵D为边AB的中点,
∴CD=AD,∠BCD=$\frac{1}{2}$∠ACB=45°,
∴∠EAD=∠FCD,
在△AED和△CFD中
$\left\{\begin{array}{l}{AD=CD}\\{∠EAD=∠CFD}\\{AE=CF}\end{array}\right.$
∴△ADE≌△CFD(SAS),
∴DE=DF,
故答案为:DE=DF;
探究:DE=DF,证明如下:
如图2,连接CD,
∵∠ACB=90°,AC=BC,
∴∠CAD=45°,
∵D为AB中点,
∴AD=CD,∠BCD=$\frac{1}{2}$∠ACB=45°,
∵∠CAD+∠EAD=∠BCD+∠FCD=180°,
∴∠EAD=∠FCD=135°,
在△ADE和△CDF中
$\left\{\begin{array}{l}{AD=CD}\\{∠EAD=∠FCD}\\{AE=CF}\end{array}\right.$
∴△ADE≌△CDF(SAS),
∴DE=DF;
应用:
∵△ADE≌△CDF,
∴∠ADE=∠CDF,
∵∠ADC=90°,
∴∠EDF=90°,
∵DE=DF=4,
∴S△DEF=$\frac{1}{2}$DE2=$\frac{1}{2}$×42=8.
点评 本题为三角形综合应用,涉及知识点有等腰直角三角形的性质、全等三角形的判定和性质及三角形的面积等.在探究中把问题转化为图1中的问题是解题的关键,即构造三角形全等.本题主要就是全等三角形的判定和性质的应用,属于基础题,难度不大.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案| A. | 对顶角相等 | |
| B. | 等角的补角相等 | |
| C. | 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行 | |
| D. | 如果一个角的两边分别平行于另一个角的两边,那么这两个角相等 |
 如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )
如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )| A. | 42° | B. | 48° | C. | 52° | D. | 58° |
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
| A. | 0 | B. | 1 | C. | -1 | D. | $\frac{1}{4}$ |
| A. | -5 | B. | 1 | C. | -1 | D. | -6 |
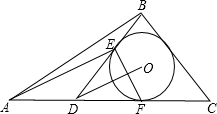 在ABC中,边AC上有一点D满足DC=2AD,O是△BDC的内心,E、F分别为⊙O与边BD、DC的切点,设BD=BC.
在ABC中,边AC上有一点D满足DC=2AD,O是△BDC的内心,E、F分别为⊙O与边BD、DC的切点,设BD=BC.