题目内容
10. 如图,在△ABC中,AB=10,AC=8,点D在边AB上,∠ACB=∠ADC,则AD的长为6.4.
如图,在△ABC中,AB=10,AC=8,点D在边AB上,∠ACB=∠ADC,则AD的长为6.4.
分析 由已知角相等,加上公共角,利用两对角相等的三角形相似得到三角形ACD与三角形ABC相似,由相似得比例求出AD的长即可.
解答 解:∵∠A=∠A,∠ACB=∠ADC,
∴△ACB∽△ADC,
∴$\frac{AC}{AB}$=$\frac{AD}{AC}$,
∵AB=10,AC=8,
∴$\frac{8}{10}$=$\frac{AD}{8}$,
则AD=6.4,
故答案为:6.4
点评 此题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
19.下列计算错误的是( )
| A. | 2m+3n=5mn | B. | a6÷a2=a4 | C. | (a2)3=a6 | D. | a•a2=a3 |
2.在△ABC中,AB=AC,BC=8,当S△ABC=20时,tanB的值为( )
| A. | $\frac{5}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
20.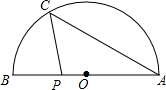 如图,AB是半圆O的直径,点C在半圆周上,连结AC,∠BAC=30°,点P是线段AB上任意一点,若AB=4,则CP的长不可能为( )
如图,AB是半圆O的直径,点C在半圆周上,连结AC,∠BAC=30°,点P是线段AB上任意一点,若AB=4,则CP的长不可能为( )
 如图,AB是半圆O的直径,点C在半圆周上,连结AC,∠BAC=30°,点P是线段AB上任意一点,若AB=4,则CP的长不可能为( )
如图,AB是半圆O的直径,点C在半圆周上,连结AC,∠BAC=30°,点P是线段AB上任意一点,若AB=4,则CP的长不可能为( )| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
 一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
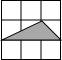
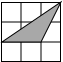
一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2. 如图,下列图中小正方形的边长为1,阴影三角形的顶点均在格点上,与△ABC相似的是( )
如图,下列图中小正方形的边长为1,阴影三角形的顶点均在格点上,与△ABC相似的是( )

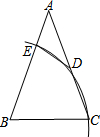 如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径作弧,分别交AC、AB于点D、E,连接DE,则∠ADE=36°.
如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径作弧,分别交AC、AB于点D、E,连接DE,则∠ADE=36°. 如图,在Rt△ABC中,∠C=90°,∠A=40°,则∠B=50°.
如图,在Rt△ABC中,∠C=90°,∠A=40°,则∠B=50°.